CBSE Class 10 Mathematics Solved Question Paper 2015

If the quadratic equation has two roots, then find the value of p.

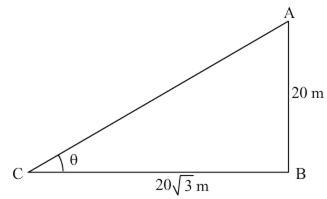
In Given figure, a tower AB is 20 m high and BC, its shadow on the ground, is m long. Find the sun's altitude.

The different dice are tossed together. Find the probability that the product of the two number on the top of the dice is 6.

In the given figure, PQ is a chord of a circle with centre O and PT is tangent. If ∠QPT = 60^o, find ∠ PRQ.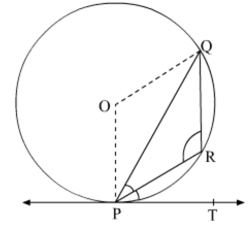

In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120^o, then prove that OR = PR + RQ.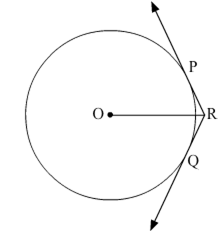

In the given figure, a triangle ABC is drawn to circumscribe of radius 3 cm, such that the segments RD and DC are respectively of length 6 cm and 9 cm. If the area of ΔABC is 54 cm², then find lengths of sides AB and AC.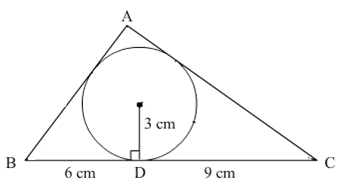

Solve the following quadratic equation for x,

4x² + 4bx - (a² - b²) = 0

In an AP, if S₅ + S₇ = 167 and S₁₀ = 235, then find the AP,  Where S_n denotes the sum of its first n terms.

The points A (4, 7), B (p, 3) and C (7, 3) are the vertices a right triangle, right-angled at B find the value of p.

Find the relation between x and y if the points A (x, y), B (-5, 7) and C (-4, 5) are collinear.