Short Answer Type
Short Answer TypeIn Fig. , PQ is tangent at point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.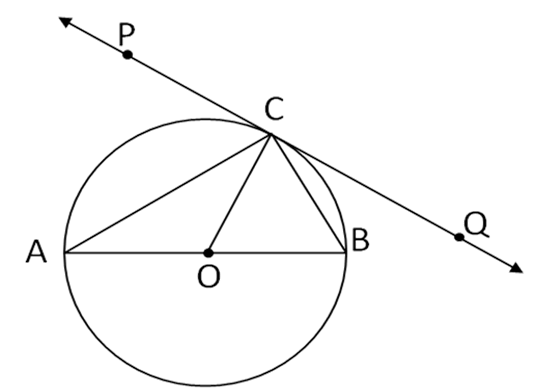
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
A card is drawn at random from a well -shuffled fled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen.
If -5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p(x2 + x)k = 0 has equal roots, find the value of k.
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
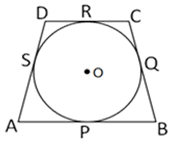
In Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.
The 4th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11th term.
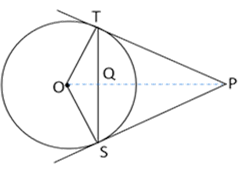
In Fig, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP=2r, show that ∠ OTS = ∠ OST = 30°.