The ratio of the height of a tower and the length of its shadow on the ground is √3:1. What is the angle of elevation of the sun?

Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of the hemisphere? 

If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?

Find the roots of the quadratic equation 

Find how many integers between 200 and 500 are divisible by 8.

Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.

Find the value of k for which the equation x² + k(2x + k − 1) + 2 = 0 has real and equal roots. 

Draw a line segment of length 8 cm and divide it internally in the ratio 4: 5.
Steps of construction.

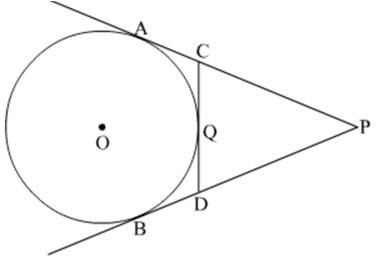
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

A number is chosen at random from the number –3, –2, –1, 0, 1, 2, 3. What will be the probability that square of this number is less then or equal to 1?