 Short Answer Type
Short Answer TypeIf the equation (1 + m2) x2 + 2mcx + c2 – a2 = 0 has equal roots then show that c2 = a2 (1 + m2).
The 3/4th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in a cylindrical vessel.
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (7/2, y), find the value of y.
Two different dice are thrown together. Find the probability that the numbers obtained
(i) have a sum less than 7
(ii) have a product less than 16
(iii) is a doublet of odd numbers.
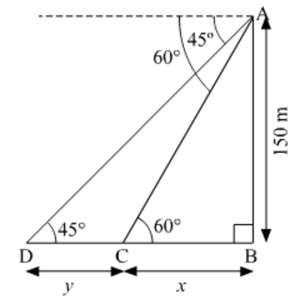
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
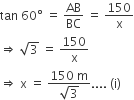
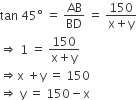
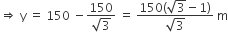
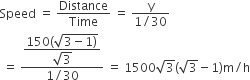
 Long Answer Type
Long Answer Type