 Long Answer Type
Long Answer TypeShow that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
How many times must a man toss a fair coin, so that the probability of having at least one head is more than 80%?
A manufacturer produces nuts and bolts. It takes 1 hours of work on machine A and 3 hours on machine B to product a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of `17.50 per package on nuts and `7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operates his machines for at the most 12 hours a day? From the above as a linear programming problem and solve it graphically.
Let the manufacturer produce x packages of nuts and y packages of bolts.
The given information can be complied in a table as follows.
| Nuts | Bolts | Availability | |
| Machine A ( h ) | 1 | 3 | 12 |
| Machine B ( h ) | 3 | 1 | 12 |
The profit on a package o nuts is Rs. 17.50 and on a package of bolts is Rs. 7.
Therefore, the constraints are
Total profit, Z = 17.5 x + 7 y
The mathematical formulation of the given problem is
Maximise Z = 17.5 x + 7 y ..............( i )
Subject to the constrain,
The feasible region determined by the system of constraints is as follows:
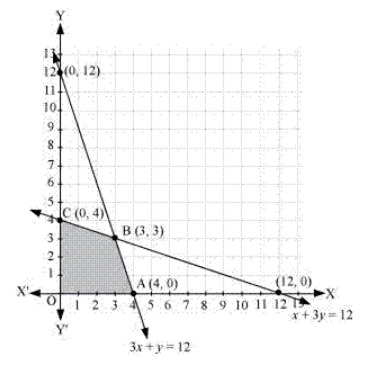
The corner points are A ( 4, 0 ), B ( 3, 3 ) and C ( 0, 4 ).
The values of Z at these corner points are as follows:
| corner point | Z = 17.5 x + 7 y | |
| O ( 0, 0 ) | 0 | |
| A ( 4, 0 ) | 70 | |
| B ( 3, 3 ) | 73.5 | Maximum |
| C ( 0, 4 ) | 28 |
The maximum values of Z is Rs. 73.50 at (3, 3 ).
Thus, 3 packages of nuts and 3 packages of bolts should be produced each day to get the maximum profit of Rs. 73.50.
