 Short Answer Type
Short Answer TypeIf A is a square matrix such that 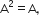 then write the value of
then write the value of 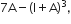 where I is an identity matrix.
where I is an identity matrix.
Given that 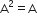
We need to find the value of 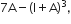 Where I is the identity matrix.
Where I is the identity matrix.
Thus, 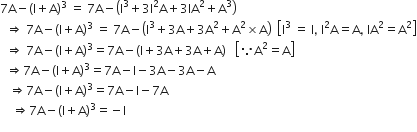
If the function f: R  R be given by
R be given by  be given by
be given by 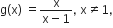 find fog and gof and hence find fog (2) and gof ( −3).
find fog and gof and hence find fog (2) and gof ( −3).
