 Short Answer Type
Short Answer TypeWrite the element  of the matrix
of the matrix  whose elements
whose elements  are given by
are given by 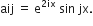
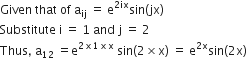
 Long Answer Type
Long Answer TypeLet A = Q × Q, where Q is the set of all rational numbers, and * be a binary operation on A defined by (a, b) * (c, d) = (ac, b+ad) for (a, b), (c, d)  A. Then find
A. Then find
(i) The identify element of * in A.
(ii) Invertible elements of A, and write the inverse of elements (5, 3) and 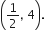
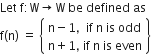
 Short Answer Type
Short Answer Type