 Short Answer Type
Short Answer Type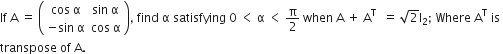
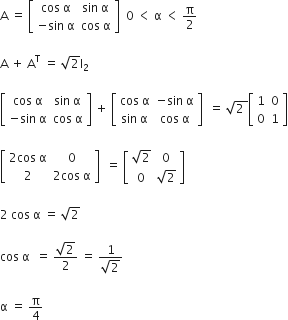
For what values of k, the system of linear equations
x + y + z = 2
2x + y - z = 3
3x + 2y + kz = 4
has a unique solution?
A typist charges Rs. 145 for typing 10 English and 3 Hindi pages, while charges for typing 3 English and 10 Hindi pages are Rs. 180. Using matrices, find the charges of typing one English and one Hindi page separately. However, typist charged only Rs. 2 per page from a poor student Shyam for 5 Hindi pages. How much less was charged from this poor boy? Which values are reflected in this problem?
Find the equation of tangents to the curve y= x3+2x-4, which are perpendicular to line x+14y+3 =0.
