 Short Answer Type
Short Answer TypeA current is induced in coil C1 due to the motion of current carrying coil C2.
(a) Write any two ways by which a large deflection can be obtained in the galvanometer G.
(b) Suggest an alternative device to demonstrate the induced current in place of galvanometer.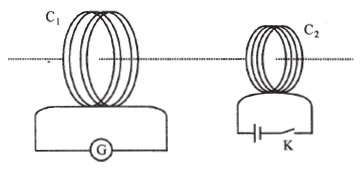
a) Two ways by which we can obtain deflection in the galvanometer is by:
i) Moving coil C2 towards C1 with high speed.
ii) By placing a soft iron laminated core at the centre of coil C1.
b) By replacing galvanometer with the torch bulb in coil C1, one can demonstrate the induced current. The bulb begins to glow as a result of the induced current.
Define the terms (i) drift velocity, (ii) relaxation time.
A conductor of length L is connected to a dc source of emf ε. If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change?Using Gauss's law obtains the expression for the electric field due to a uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric field with r, for r > R and r < R.
In the circuit shown, R1 = 4 Ω, R2 = R3 = 15 Ω, R4 = 30 Ω and E = 10 V. Calculate the equivalent resistance of the circuit and the current in each resistor.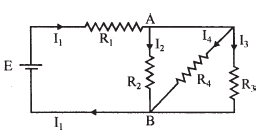
State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying current behave as a magnet?With the help of a labelled diagram, state the underlying principle of a cyclotron. Explain clearly how it works to accelerate the charged particles.
Show that cyclotron frequency is independent of energy of the particle. Is there an upper limit on the energy acquired by the particle? Give reason.Show graphically, the variation of the de-Broglie wavelength ( λ ) with the potential ( V ) through which an electron is accelerated from rest.
In a transistor, doping level in base is increased slightly. How will it affect (i) collector current and (ii) base current?
When monochromatic light travels from one medium to another its wavelength changes but frequency remains the same, Explain.
Two convex lenses of same focal length but of aperture A1 and A2 (A2 < A1), are used as the objective lenses in two astronomical telescopes having identical eyepieces. What is the ratio of their resolving power? Which telescope will you prefer and why? Give reason.
