 Short Answer Type
Short Answer TypeTwo charges of magnitudes – 2Q and + Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
Using gauss law, we have![]()
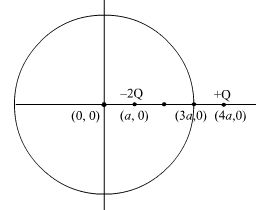
Electric flux is given by, ![]()
How does the mutual inductance of a pair of coils change when,
(i) distance between the coils is increased and
(ii) number of turns in the coils is increased?
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance?
The motion of copper plate is damped when it is allowed to oscillate between the two poles of a magnet. What is the cause of this damping?
Welders wear special goggles or face masks with glass windows to protect their eyes from electromagnetic radiations. Name the radiations and write the range of their frequency.
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
A capacitor, made of two parallel plates each of plate area A and separation d, is being charged by an external ac source. Show that the displacement current inside the capacitor is the same as the current charging the capacitor.
Explain the term ‘drift velocity’ of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of ‘drift velocity’.
Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a cell.
(a) For a given a.c.,
(b) A light bulb is rated at 100 W for a 220 V a.c. supply. Calculate the resistance of the bulb.
