Short Answer TypeThe resistance offered by the capacitor when connected to an electrical circuit is known as capacitive reactance.
It is given by,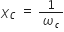
where,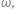 
is the angular frequency of the source, and
C, is the capacitance of the capacitor.
SI Unit is ohm.
Graph showing the variation of current versus voltage for a material GaAs is shown in the figure. Identify the region of
i) negative resistance
ii) where Ohm’s law is obeyed.
Name the parts of the electromagnetic spectrum which is
(a) suitable for radar systems used in aircraft navigation.
(b) used to treat muscular strain.
(c) used as a diagnostic tool in medicine.
Write in brief, how these waves can be produced.A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus
(i) R and
(ii) the current I.
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also, calculate the charge on each capacitor in parallel combination.
State the principle of working of a galvanometer.
A galvanometer of resistance G is converted into a voltmeter to measure upto V volts by connecting a resistance R1 in series with the coil. If a resistance R2 is connected in series with it, then it can measure upto V/2 volts. Find the resistance, in terms of R1 and R2, required to be connected to convert it into a voltmeter that can read upto 2 V. Also find the resistance G of the galvanometer in terms of R1 and R2.An inductor L of inductance XL is connected in series with a bulb B and an ac source.
How would brightness of the bulb change when (i) number of turn in the inductor is reduced, (ii) an iron rod is inserted in the inductor and (iii) a capacitor of reactance XC = XL is inserted in series in the circuit. Justify your answer in each case.
Switch
