 Short Answer Type
Short Answer TypeObtain the relation between the decay constant and half-life of a radioactive sample.
The half-life of a certain radioactive material against  decay is 100 days. After how much time, will the undecayed fraction of the material be 6.25%?
decay is 100 days. After how much time, will the undecayed fraction of the material be 6.25%?
In a radioactive sample, number of atoms at any instant is given by, 
Now, when t = T, where T is the half-life of the sample.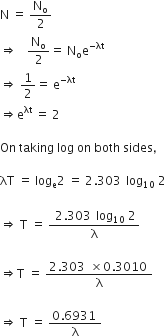
This implies, half-life of a radioactive substance is inversely proportional to decay constant.
Numerical:
We have,
Number of undecayed nuclei left = 6.25 % = 6.25/ 100 = 1/16
Let, t be the required time after which the undecayed fraction of the material will be 6.25%.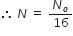
(a) Define the term 'intensity of radiation' in terms of photon picture of light.
(b) Two monochromatic beams, one red and the other blue, have the same intensity.
In which case:
(i) the number of photons per unit area per second is larger,
(ii) the maximum kinetic energy of the photoelectrons is more? Justify your answer.
 Long Answer Type
Long Answer TypeDuring a thunderstorm the 'live' wire of the transmission line fell down on the ground from the poles in the street. A group of boys, who passed through, noticed it and some of them wanted to place the wire by the side. As they were approaching the wire and trying to lift the cable, Anuj noticed it and immediately pushed them away, thus preventing them from touching the live wire. During pushing some of them got hurt. Anuj took them to a doctor to get them medical aid.
Based on the above paragraph, answer the following questions:
(a) Write the two values which Anuj displayed during the incident.
(b) Why is it that a bird can sit on a suspended 'live' wire without any harm whereas touching it on the ground can give a fatal shock?
(c) The electric power from a power plant is set up to a very high voltage before transmitting it to distant consumers. Explain, why.a) State Kirchhoff's rules and explain on what basis they are justified.
(b) Two cells of emfs E1 and E2 and internal resistances r1 and r2 are connected in parallel.
Derive the expression for the
(i) Emf and
(ii) internal resistance of a single equivalent cell which can replace this combination.
OR
(a) 'The outward electric flux due to charge +Q is independent of the shape and size of the surface which encloses is.' Give two reasons to justify this statement.
(b) Two identical circular loops '1' and '2' of radius R each have linear charge densities -![]() and +
and +![]() C/m respectively. The loops are placed coaxially with their centre distance apart. Find the magnitude and direction of the net electric field at the centre of loop '1'.
C/m respectively. The loops are placed coaxially with their centre distance apart. Find the magnitude and direction of the net electric field at the centre of loop '1'.
Two infinitely long straight parallel wires, '1' and '2', carrying steady currents I1 and I2 in the same direction are separated by a distance d. Obtain the expression for the magnetic field due to the wire '1' acting on wire '2'. Hence find out, with the help of a suitable diagram, the magnitude and direction of this force per unit length on wire '2' due to wire '1'. How does the nature of this force changes if the currents are in opposite direction? Use this expression to define the S.I. unit of current.
Draw a necessary arrangement for winding of primary and secondary coils in a step-up transformer. State its underlying principle and derive the relation between the primary and secondary voltages in terms of number of primary and secondary turns. Mention the two basic assumptions used in obtaining the above relation.
State any two causes of energy loss in actual transformers.
(a) Use Huygens' principle to show the propagation of a plane wavefront from a denser medium to a rarer medium. Hence find the ratio of the speeds of wavefront in the two media.
(b) (i) Why does an unpolarized light incident on a polaroid get linearly polarized ?
(ii) Derive the expression of Brewster's law when unpolarized light passing from a rarer to a denser medium gets polarized on reflection at the interface.
A biconvex lens with its two faces of equal radius of curvature R is made of a transparent medium of refractive index ![]() 1. It is kept in contact with a medium of refractive index 2 as shown in the figure.
1. It is kept in contact with a medium of refractive index 2 as shown in the figure.
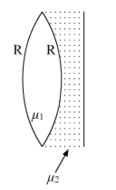
a) Find the equivalent focal length of the combination.
b) Obtain the condition when this combination acts as a diverging lens.
c) Draw the ray diagram for the case ![]() when the object is kept far away from the lens. Point out the nature of the image formed by the system.
when the object is kept far away from the lens. Point out the nature of the image formed by the system.
