Short Answer Type
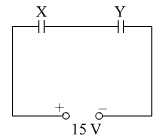
Short Answer TypeA point charge +Q is placed at point O as shown in the figure. Is the potential
difference VA – VB is positive, negative or zero?
Electric potential at a distance r from the point charge +Q is given by,
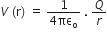
Potential at point A is, 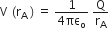
Similarly, potential at point B is given by, 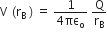
Since rA < rB 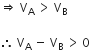
a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
b) A neutron, an electron and an alpha particle, moving with equal velocities, enter a uniform magnetic field going into the plane of paper, as shown. Trace their paths in the field and justify your answer. 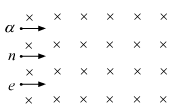
i) Define mutual Inductance.
ii) A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes 20 A in 0.5 s, what is the change of flux linkage with the other coil?