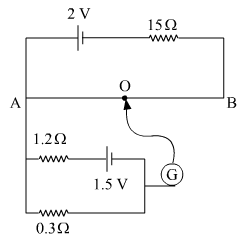
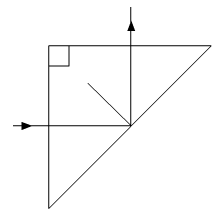
Short Answer Type
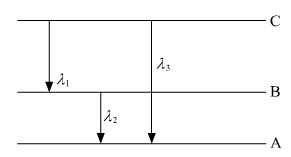
Bohr's Quantisation Rule:
According to Bohr, an electron can revolve only in certain discrete, non-radiating orbits for which the total angular momentum of the revolving electron is an integral multiple of 
; where h is the Planck's constant.
That is,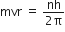 
b)
Using Rydberg's formula for spectra of hydrogen atom, we have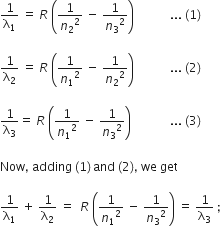
Hence, the relation between 3 wavelengths from the energy-level diagram is obtained.
Long Answer Type(i) An a.c. source of voltage V = Vo sin ωt is connected to a series combination of L, C and R. Use the phasor diagram to obtain an expression for impedance of a circuit and the phase angle between voltage and current. Find the condition when current will be in phase with the voltage. What is the circuit in this condition called?
ii) In a series LR circuit, XL = R and the power factor of the circuit is P1. When capacitor with capacitance C, such that XL = XC is put in series, the power factor becomes P2. Calculate P1 / P2.
(i) Write the function of a transformer. State its principle of working with the help of a diagram. Mention various energy losses in this device.
(ii) The primary coil of an ideal step-up transformer has 100 turns and the transformation ratio is also 100. The input voltage and power are 220 V and 1100 W, respectively. Calculate the:
a) number of turns in secondary
b) current in primary
c) voltage across secondary
d) current in secondary
e) power in secondary
(i) Define the term drift velocity.
(ii) On the basis of electron drift, derive an expression for resistivity of a conductor in terms of number density of free electrons and relaxation time. On what factors does resistivity of a conductor depend?
(iii) Why alloys like constantan and manganin are used for making standard resistors?
Switch
