 Short Answer Type
Short Answer TypeDoes the charge given to a metallic sphere depend on whether it is hollow or solid? Give a reason for your answer.
No, Because the charge resides only on the surface of the conductor.
A long straight current carrying wire passes normally through the centre of the circular loop. If the current through the wire increases, will the be an induced emf in the loop? Justify
At a place, the horizontal component of earth's magnetic field is B and angle of dip are 60o. What is the value of a horizontal component of the earth's magnetic field at the equator?
How does Ampere-Maxwell law explain the flow of current through a capacitor when it is being charged by a battery? Write the expression for the displacement current in terms of the rate of change of electric flux.
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase: current or voltage?
(ii) Without making any other change, find the value of the additional capacitor C, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.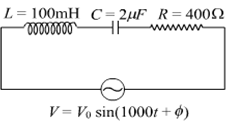
A resistance of R draws current from a potentiometer. The potentiometer wire, AB, has a total resistance of Ro. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of potentiometer wire.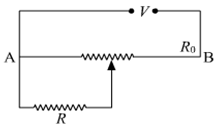
(i) Find equivalent capacitance between A and B in the combination given below. Each capacitor is of 2μF capacitance.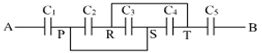
Drive the expression for electric field at a point on the equatorial line of an electric dipole.
Depict the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
