 Long Answer Type
Long Answer TypeDescribe the working principle of a moving coil galvanometer.
Why is it necessary to use
(i) a radial magnetic field and
(ii) a cylindrical soft iron core in a galvanometer?
Write the expression for the current sensitivity of the galvanometer.
Can a galvanometer as such be used for measuring the current? Explain.
Moving coil galvanometer is an instrument used for the detection and measurement of small currents. 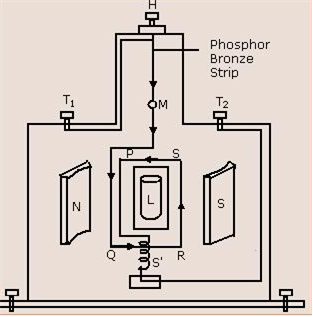
Principle: The working of moving coil galvanometer is that when a current carrying coil is placed in a varying magnetic field, it experiences torque.
Consider a rectangular coil for which no. of turns = N
Are of cross-section is A = lb
Intensity of the uniform magnetic field = B
Current through the coil = I
Therefore,
Deflecting torque is given by,
BIL x b = BIA
For N number of turns,
![]() = NBIA
= NBIA
Restoring torque in the spring = k![]()
Therefore, 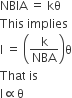
i) The soft iron coil in a galvanometer will make the field radial. Also, it increases the strength of the magnetic field.
ii) Current sensitivity in the galvanometer is given by, ![]()
Voltage sensitivity in the galvanometer is given by, ![]()
Yes a galvanometer can be used for measuring the current.
(a) Define the term 'self-inductance' and write its S.I. unit.
(b) Obtain the expression for the mutual inductance of two long co-axial solenoids S1 and S2 wound one over the other, each of length L and radii r1 and r2 and n1 and n2 number of turns per unit length when a current I is set up in the outer solenoid S2.
(a) Draw a labelled diagram of a step-up transformer. Obtain the ratio of secondary to primary voltage in terms of number of turn and currents in the two coils.
(b) A power transmission line feeds input power at 2200 V to a step-down transformer with its primary windings having 300 turns. Find the number of turns in the secondary to get the power output at 220 V.
Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm's law.
The current is drawn from a cell of emf E and internal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for (i) the current draw from the cell and (ii) the power consumed in the network.
(i) A ray of light incident on face AB of an equilateral glass prism shows the minimum deviation of 30°. Calculate the speed of light through the prism.
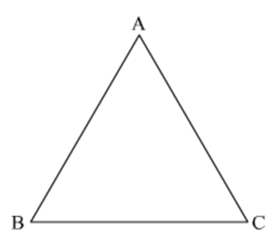
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
