 Short Answer Type
Short Answer TypeThe teachers of Geeta’s school took the students on a study trip to a power generating station, located nearly 200 km away from the city. The teacher explained that electrical energy is transmitted over such a long distance to their city, in the form of alternating current (ac) raised to a high voltage. At the receiving end in the city, the voltage is reduced to operate the devices. As a result, the power loss is reduced. Geeta listened to the teacher and asked questions about how the ac is converted to a higher or lower voltage.
Define electric flux. Is it a scalar or a vector quantity?
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss’ law to obtain the expression for the electric flux through the square.
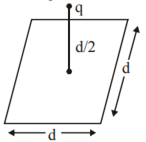
b) If the point charge is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.
a) Use Gauss’ law to derive the expression for the electric field due to a straight uniformly charged infinite line of charge density λ C/m.
(b) Draw a graph to show the variation of E with perpendicular distance r from the line of charge.
(c) Find the work done in bringing a charge q from perpendicular distance r1 to r2 (r2>r1).
State the principle of an ac generators and explain its working with the help of a labelled diagram. Obtain the expression for the emf induced in a coil havin N turns each of cross-sectional area, rotating with a constant angular speed 'ω' in a magnetic field , directed perpendicular to the axis of rotation.
An aeroplane is flying horizontally from west to east with a velocity of 900 km/hour. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth’s magnetic field is 5 × 10–4 T and the angle of dip is 30°.
A device X is connected across an ac source of voltage V=V0sin ωt. The current through X is given as
A proton and an electron travelling along parallel paths enter a region of uniform magnetic field, acting perpendicular to their paths. Which of them will move in a circular path with higher frequency ?
Draw graphs showing a variation of the photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
Four nuclei of an element undergo fusion to form a heavier nucleus, with the release of energy. Which of the two — the parent or the daughter nucleus — would have higher binding energy per nucleon?
