 Multiple Choice Questions
Multiple Choice QuestionsThe angle between the lines 2x = 3y = − z and 6x = − y = − 4z is
0o
90o
45o
45o
B.
90o
Angle between the lines 2x = 3y = - z & 6x = -y = -4z is 90°
Since a1a2 + b1b2 + c1c2 = 0
If the plane 2ax − 3ay + 4az + 6 = 0 passes through the midpoint of the line joining the centres of the spheres
x2 + y2 + z2 + 6x − 8y − 2z = 13 and x2 + y2 + z2 − 10x + 4y − 2z = 8, then a equals
-1
1
-2
-2
If a vertex of a triangle is (1, 1) and the mid-points of two sides through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is
(-1, 7/3)
(-1/3, 7/3)
(1, 7/3)
(1, 7/3)
Let a, b and c be distinct non-negative numbers. If the vectors 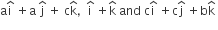
the Geometric Mean of a and b
the Arithmetic Mean of a and b
equal to zero
equal to zero
If 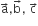 are non -coplanar vector λ is a real number then
are non -coplanar vector λ is a real number then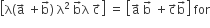
exactly one value of λ
no value of λ
exactly three values of λ
exactly three values of λ
Three houses are available in a locality. Three persons apply for the houses. Each applies to one house without consulting others. The probability that all the three apply for the same house is
2/9
1/9
8/9
8/9
