Suppose a population A has 100 observations 101, 102, … , 200, and another population B has 100 observations 151, 152, … , 250. If VA and VB represent the variances of the two populations, respectively, then V_A/V_B is 

• 1

• 9/4

• 4/9

• 4/9

If the roots of the quadratic equation x² + px + q = 0 are tan30° and tan15°, respectively then the value of 2 + q − p is

• 2

• 3

• 0

• 0

Let W denote the words in the English dictionary. Define the relation R by :
R = {(x, y) ∈ W × W | the words x and y have at least one letter in common}. Then R is

• not reflexive, symmetric and transitive

• reflexive, symmetric and not transitive

• reflexive, symmetric and transitive

• reflexive, symmetric and transitive

The value of 

• i

• 1

• -i

• -i

All the values of m for which both roots of the equations x² − 2mx + m² − 1 = 0 are greater than −2 but less than 4, lie in the interval

• −2 < m < 0

• m > 3

• −1 < m < 3 

• −1 < m < 3 

A body falling from rest under gravity passes a certain point P. It was at a distance of 400 m from P, 4s prior to passing through P. If g = 10 m/s² , then the height above the point P from where the body began to fall is

• 720 m

• 900 m

• 320 m

• 320 m

A straight line through the point A(3, 4) is such that its intercept between the axes is bisected at A. Its equation is

• x + y = 7

• 3x − 4y + 7 = 0

• 4x + 3y = 24

• 4x + 3y = 24

The two lines x = ay + b, z = cy + d; and x = a′y + b′, z = c′y + d′ are perpendicular to each other if

• aa′ + cc′ = −1

• aa′ + cc′ = 1

• 
• 

The locus of the vertices of the family of parabolas 

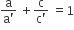
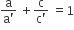
In an ellipse, the distance between its foci is 6 and minor axis is 8. Then its eccentricity is

• 3/5

• 1/5

• 2/5

• 2/5