 Multiple Choice Questions
Multiple Choice QuestionsIf, for a positive integer n, the quadratic equation,
x(x + 1) + (x + 1) (x + 2) + .....
+ (x + n -1 ) (x + n) = 10n
has two consecutive integral solutions, then n is equal to :
11
12
9
9
The function 
neither injective nor surjective.
invertible
injective but not surjective.
injective but not surjective.
The following statement
(p → q ) → [(~p → q) → q] is
a fallacy
a tautology
equivalent to ~ p → q
equivalent to ~ p → q
For any three positive real numbers a, b and c, (25a2 + b2) + 25(c2 – 3ac) = 15b(3a + c), Then
b , c and a are in G.P
b, c and a are in A.P
a, b and c are in A.P
a, b and c are in A.P
hyperbola passes through the point P(√2, √3) and has foci at (± 2, 0). Then the tangent to this hyperbola at P also passes through the point
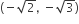
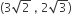
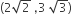
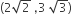
Let a, b, c ∈ R. If f(x) = ax2 + bx + c is such
that a + b + c = 3 and f(x + y) = f(x) + f(y) + xy, ∀x,y ∈ R,then 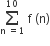 is equal to
is equal to
225
330
165
165
Twenty meters of wire is available for fencing off a flower-bed in the form of a circular sector.Then the maximum area (in sq. m) of the flower-bed, is
30
12.5
10
10
The value of
(21C1 – 10C1) + (21C2 – 10C2) + (21C3 – 10C3) + (21C4 – 10C4) + .... +
(21C10 – 10C10) is
220 – 210
221 – 211
221 – 210
221 – 210