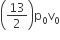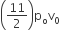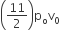Multiple Choice Questions
Multiple Choice QuestionsA metallic rod of length ‘l’ is tied to a string of length 2l and made to rotate with angular speed ω on a horizontal table with one end of the string fixed. If there is a vertical magnetic field ‘B’ in the region, the e.m.f. induced across the ends of the rod is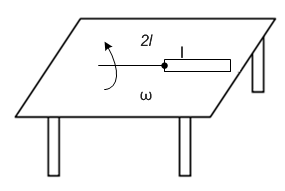
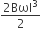
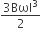
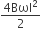
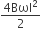
This question has Statement I and Statement II. Of the four choices given after the Statements, choose the
one that best describes the two Statements.
Statement – I: A point particle of mass m moving with speed v collides with stationary point particle of mass M. If the maximum energy loss possible is given as f 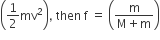
Statement – II : Maximum energy loss occurs when the particles get stuck together as a result of the collision.
Statement – I is true, Statement – II is true, Statement – II is a correct explanation of Statement – I.
Statement – I is true, Statement – II is true, Statement – II is not a correct explanation of Statement – I.
Statement – I is true, Statement – II is false.
Statement – I is true, Statement – II is false.
Let [ε0] denote the dimensional formula of the permittivity of vacuum. If M = mass, L = length, T = time and A = electric current, then
[ε0] = [M-1L-3T2A]
[ε0] = [M-1L-3T4A2]
[ε0] =[M-2L2T-1A-2]
[ε0] =[M-2L2T-1A-2]
A projectile is given an initial velocity of where is along the ground and
where is along the ground and  is along the vertical. If g = 10 m/s2, the equation of its trajectory is:
is along the vertical. If g = 10 m/s2, the equation of its trajectory is:
y = x-5x2
y = 2x-5x2
4y = 2x- 5x2
4y = 2x- 5x2
What is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
5GmM/6R
2GmM/3R
GmM/2R
GmM/2R
A hoop of radius r and mass m rotating with an angular velocity ω0
is placed on a rough horizontal surface.The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?
rω0/4
rω0/3
rω0/2
rω0/2
A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density σ at the equilibrium position. The extension x0 of the spring when it is in equilibrium is
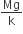
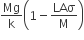
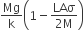
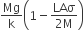
The amplitude of a damped oscillator decreases to 0.9 times its original magnitude is 5s. In another 10s it will decrease to α times its original magnitude, where α equals
0.7
0.81
0.729
0.729
A sonometer wire of length 1.5 m is made of steel. The tension in it produces an elastic strain of 1 %. What is the fundamental frequency of steel if density and elasticity of steel are 7.7 × 103 kg/m3 and 2.2 × 1011N/m2 respectively?
188.5 Hz
178.2 Hz
200.5 Hz
200.5 Hz
The above p-v diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat extracted from the source in a single cycle is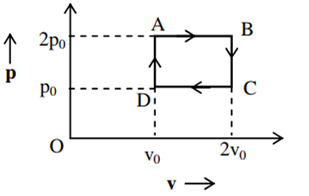
povo