 Multiple Choice Questions
Multiple Choice QuestionsFrom the tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle to hit the ground is n times that taken by it to reach the highest point of its path. The relation between H,u and n is
2gH = n2u2
gH = (n-2)2u2
2gH = nu2(n-2)2u2
2gH = nu2(n-2)2u2
C.
2gH = nu2(n-2)2u2
Time is taken to reach the maximum height t1 = u/g
If t2 is the time taken to hit the ground,
i.e, 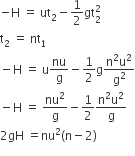
A mass ‘m’ is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?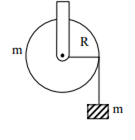
2g/3
g/2
5g/6
5g/6
A block of mass m is placed on a surface with a vertical cross-section given by y = x3/6. If the coefficient of friction is 0.5, the maximum height above ground at which the block can be placed without slipping is
When a rubber band is strecthed by a distance x, it exerts a restoring force of magnitude F = ax +bx2, where a and b are constants. The work done in stretching are unstretched rubber-band by L is
aL2 +bL2
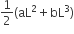
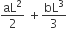
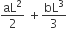
A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical. About the point of suspension
angular momentum is conserved
angular momentum changes in magnitude but not in the direction
angular momentum changes in direction but not in magnitude
angular momentum changes in direction but not in magnitude
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
![]()
![]()
![]()
![]()
A student measured the length of a rod and wrote it as 3.50 cm. Which instrument did he use to measure it?
A meter scale.
A vernier calliper where the 10 divisions in vernier scale match with 9 division in the main scale and main scale have 10 divisions in 1 cm.
A screw gauge having 100 divisions in the circular scale and pitch as 1 mm.
A screw gauge having 100 divisions in the circular scale and pitch as 1 mm.
The pressure that has to be applied to the ends of a steel wire of length 10 cm to keep its length constant when its temperature is raised by 100°C is (For steel Young’s modulus is 2×1011 N m–2 and coefficient of thermal expansion is 1.1×10–5 K–1 )
2.2 x 108 Pa
2.2 x 109 Pa
2.2 x 107 Pa
2.2 x 107 Pa
There is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1 and d2 are filled in the tube. Each liquid subtends 90o angle at centre. Radius joining their interface makes an angle α with vertical. ratio d1/d2 is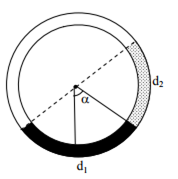
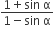
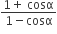


On the heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r < < R and the surface tension of water is T, value of r just before bubbles detach is (density of water is ρw)
![]()
![]()
![]()
![]()
