 Multiple Choice Questions
Multiple Choice Questions‘n’ moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be: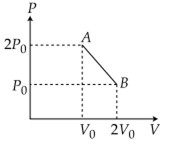
![]()
![]()
![]()
![]()
A.
![]()
As, T will be maximum temperature where product of pV is maximum
Equation of line AB, we have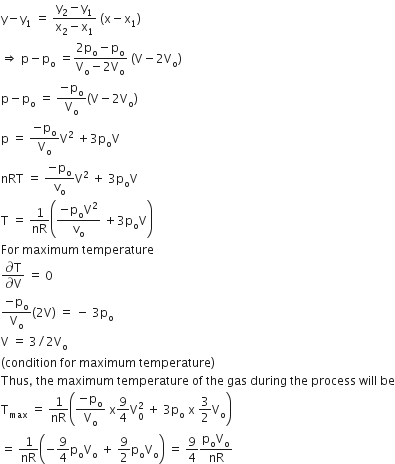
A particle performs simple harmonic motion with amplitude A. It's speed is trebled at the instant that it is at a distance 2A/3 from the equilibrium position. The new amplitude of the motion is:

3A


The region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density ρ = A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is: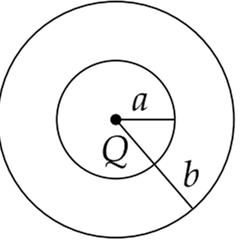

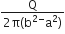
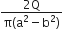
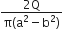
A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the 4 µF and 9 µF capacitors), at a point distant 30 m from it, would equal: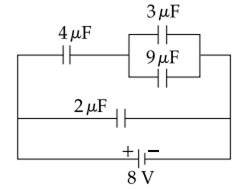
240N/C
360N/C
420N/C
420N/C
Two identical wires A and B, each of length ‘l’, carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side ‘a’. If BA and BB are the values of the magnetic field at the centres of the circle and square respectively, then the ratio BA /BB is:
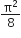
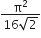
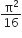
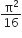
Hysteresis loops for two magnetic materials A and B are given below: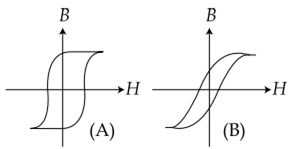
These materials are used to make magnets for electric generators, transformer core and electromagnet core. Then it is proper to use:
A for electric generators and transformers.
A for electromagnets and B for electric generators
A for transformers and B for electric generators.
A for transformers and B for electric generators.
An arc lamp requires a direct current of 10 A at 80 V to function. If it is connected to a 220 V (rms), 50 Hz AC supply, the series inductor needed for it to work is close to:
80 H
0.08 H
0.044 H
0.044 H
A galvanometer having a coil resistance of 100 Ω gives a full-scale deflection, when a current of 1 mA is passed through it. The value of the resistance, which can convert this galvanometer into ammeter giving a full-scale deflection for a current of 10 A, is:
0.01 Ω
2 Ω
0.1 Ω
0.1 Ω
The temperature dependence of resistances of Cu and undoped Si in the temperature range 300-400 K is best described by:
Linear increase for Cu, linear increase for Si.
Linear increase for Cu, exponential increase for Si.
Linear increase for Cu, exponential decrease for Si.
Linear increase for Cu, exponential decrease for Si.
Arrange the following electromagnetic radiations per quantum in the order of increasing energy:
A: Blue light
B: Yellow light
C: X-ray
D: Radiowave
D, B, A, C
A, B, D, C
C, A, B, D
C, A, B, D
