 Multiple Choice Questions
Multiple Choice QuestionsThe additional kinetic energy to be provided to a satellite of mass m revolving around a planet of mass M, to transfer it from a circular orbit of radius R1 to another of radius R2(R2> R1) is

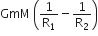
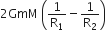
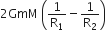
The speed of the projectile at its maximum height is half of its initial speed. The angle of projection is
60o
15o
30o
30o
From a circular disc of radius R and mass 9M, a small disc of mass M and radius R/3 is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
40MR2/9
MR2
4 MR2
4 MR2
A particle moves in the x-y plane according to rule x = a sin ωt and y = a cos ωt. The particle follows
an elliptical path
a circular path
a parabolic path
a parabolic path
A closely wound solenoid of 2000 turns and area of cross -section 1.5 x 10-4 m2 carries a current of 2.0 A. It is suspended through its centre and perpendicular to its length, allowing it to turn in a horizontal plane in a uniform magnetic field 5 x 10-2 T making an angle of 30o with axis of the solenoid. The torque on the solenoid will be
3 x 10-3 N-m
1.5 x 10-3 N-m
1.5 x 10-2 N-m
1.5 x 10-2 N-m
(1) Centre a gravity (CG) of a body is the point at which the weight of the body acts.
(2) Centre of mass coincides with the centre of gravity if the earth is assumed to have infinitely large radius
(3) To evaluate the gravitational field intensity due to anybody can be considered to be concentrated at its CG.
(4) The radius of gyration of anybody rotating about an axis is the length of the perpendicular dropped from the CG of the body to the axis.
Which one of the following pairs of statements is correct?
(4) and (1)
(1) and (2)
(2) and (3)
(2) and (3)
A thin circular ring of mass M and radius r is rotating about its axis with constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with angular velocity given by
(M +2m)ω /2m
2Mω / M + 2m
(M +2m)ω / M
(M +2m)ω / M
A student measures the distance traversed in free fall of a body, initially at rest in a given time. He uses this data to estimate g, the acceleration due to gravity. If the maximum percentage errors in measurement of the distance and the time are e1 and e2 respectively, the percentage error in the estimation of g is
e1 - e2
e1 + 2e2
e1+ e2
e1+ e2
The dependence of acceleration due to gravity g on the distance r from the centre of the earth assumed to be a sphere of radius R of uniform density is as shown in figure below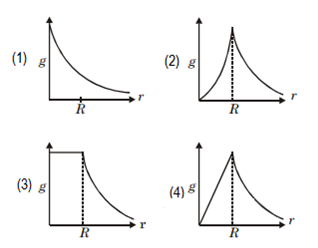
The correct figure is
(4)
(1)
(2)
(3)
If Cp- Cv denote the specific heats (per unit mass) of an ideal gas of molecular weight M
Here R is the molar gas constant
Cp-CV = R/M2
Cp-CV = R
Cp-CV = R/M
Cp-CV = R/M