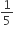Multiple Choice Questions
Multiple Choice QuestionsA General, while arranging his men, who were 6000 in number, in the form of a square, found that there were 71 men left over. How many were arranged in each row?
73
77
87
87
A number, when divided successively by 4, 5 and 6 leaves remainders 2, 3 and 4 respectively. The least such number is
50
53
56
58
A number, when divided by 296, gives 75 as the remainder. If the same number is divided by 37 then the remainder will be
1
2
19
19
The sum and product of two numbers are 12 and 35 respectively. The sum of their reciprocals will be