 Multiple Choice Questions
Multiple Choice QuestionsSummative Assessment of the unit'Mensuration' can be done through
paper-pencil test
ICT activity
project work
maths lab activity
A student observed the following examples
(10)2
= (5+5)2 = 52 + 2(5)(5) + (5)2 = 100
= (6+4)2 = 62 + 2(6)(4) + (4)2 = 100
= (8+2)2 = 82 + 2(8)(2) + (2)2 = 100
= (1+9)2 = 12 + 2(1)(9) + (9)2 = 100
and concluded that
(a +b)2 =a2+2(a)(b) + b2
The above method of drawing conclusions is
analytical
activity
deductive
inductive
A suitable approach to introduce Coordinate Geometry in Class IX is through the use of demonstration using
technology integration
solving problems
lecture method
role play
Ankur got zero marks in a word problem on linear equations in an assessment. The teacher knows that he can solve linear equations correctly. The teacher ought to remark in his report
Ankur has a problem in comprehending the language of the question, though he can solve the equations
Ankur lacks concentration and hence has examination phobia
Ankur is not studying and practising at home
Ankur has not understood the concept of linear equations completely
While teaching ratio and proportion, Ms Rama demonstrated some computer operations on the screen - 'copy and paste' and 'copy and enlarge' or 'copy and reduce'. This activity maybe
formative assessment activity
fun activity to pass time
pre-content activity to introduce ratio
post-content activity
A large basket of fruits contains 3 oranges, 2 apples and 5 bananas. If a piece of fruit is chosen at random, what is the probability of getting an orange or a banana?
The symbol ![]() drawn to any size means a + 4 and the symbol
drawn to any size means a + 4 and the symbol ![]() drawn to any size means b2, where a and b are numbers. Then, the value of
drawn to any size means b2, where a and b are numbers. Then, the value of
![]()
32
9
75
35
While solving a problem based on 'Pythagoras theorem', a teacher draws the following ABC.
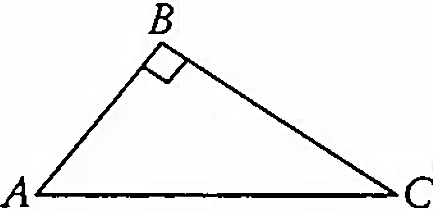
Rajan argued that the ABC is not drawn correctly. The only way to draw is
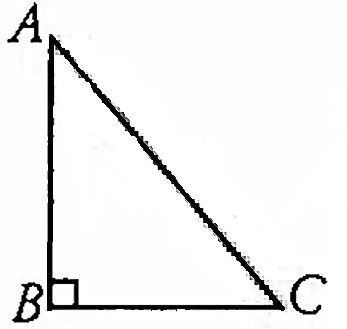
Rajan has the misconception as
he has dysgraphia
he lacks in analytical ability
he is weak in geometrical concepts
his teacher must have always drawn the triangle in this particular way