The centre of a circle is (2α - 1, 7) and it passes through the point (- 3, - 1). If the diameter of the circle is 20 units, then find the value(s) of α.

Let co-ordinates of centre be 0(2α - 1,7), which passes through the point A(- 3, - 1).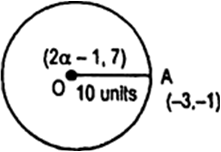

Fig. 7.23(A)
Now OA = 10 units

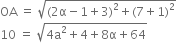
$OA space equals space square root of left parenthesis 2 straight alpha minus 1 plus 3 right parenthesis squared plus left parenthesis 7 plus 1 right parenthesis squared end root 10 space equals space square root of 4 straight a squared plus 4 plus 8 straight alpha plus 64 end root$

Squaring
100 = 4α² + 8α + 68
4α² + 8α - 32 = 0
α² + 2α - 8 = 0
α² + 4α + 2α - 8 = 0
α(α + 4) + 2(α - 8) = 0
(α - 4) (α - 2) = 0
α = -4, α = 2.

1083 Views

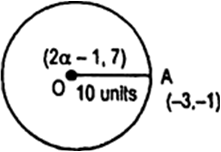
Coordinate Geometry

Hope you found this question and answer to be good. Find many more questions on Coordinate Geometry with answers for your assignments and practice.

Mathematics

Browse through more topics from Mathematics for questions and snapshot.