The houses in a row numbered consecutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses preceding the house numbered X is equal to the sum of the numbers of houses following X.

Let there be a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it.

That is , 1+2+3+......+(x-1) =(x-1)+(x+2)+.....+49
therefore,
1+2+3+.....+(x-1)
=[1+2+.....+x+(x+1)+.....+49]-(1+2+3+....+x)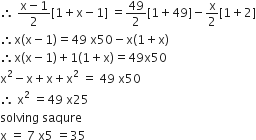

Since x is not a fraction, the value of x satisfying the given condition exists and is equal to 35.