Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.

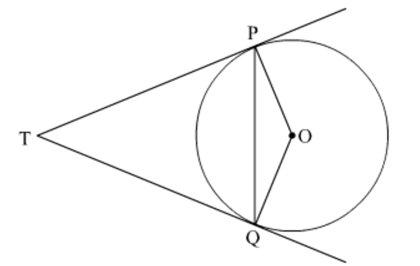
Given: TP and TQ are two tangents of a circle with centre O and P and Q are points of contact
To prove: ∠PTQ=2∠OPQ
Suppose ∠PTQ=θ.
Now by theorem, "The lengths of tangents drawn from an external point to a circle are equal".
So, TPQ is an isosceles triangle.
Therefore, ∠TPQ=∠TQP=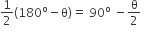
Also by theorem "The tangents at any point of a circle is perpendicular to the radius through the point of contact" ∠OPT=90°.
Therefore,
∠OPQ=∠OPT−∠TPQ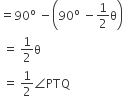


Hence, ∠PTQ=2∠OPQ.