If both (x - 2) and  are factors of px² + 5x + r, show that p = r.

Let f(x) = px² + 5 x + r
If (x - 2) is a factor of f (x), then by factor theorem
f(2) = 0 | x - 2 = 0 ⇒ x = 2
⇒ p(2)² + 5(2) + r = 0
⇒ 4p + r + 10 = 0    ...(1)

If  is a factor of f (x), then by factor theorem,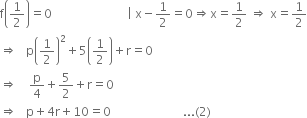

Subtracting (2) from (1), we get
3p - 3r = 0
⇒    p = r