For a convex mirror, prove that its focal length is equal to half of its radius of curvature.

---

Relation between f and R for convex mirror: As shown in Fig, consider a ray AB parallel to the principal axis and incident at the point B of a convex mirror. After reflection from the mirror, the ray appears to come from focus F.


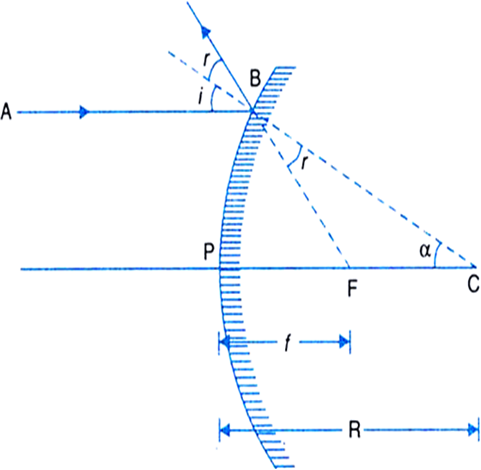
Fig. Relation between f and R for a convex mirror
If C is the centre of curvature, then PC = R, is the radius of the curvature and CB is the normal to the mirror at point B. According to the law of reflection,
∠i = ∠r
As AB is parallel to PC, so
∠i = ∠α (Corresponding angles)
∴ ∠ α = ∠ r
Thus ∆ BCF is isosceles. Hence, BF = FC.
If the aperture of the mirror is small, then B lies close to P, so that
                       
                  
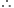
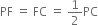
or                        
or