Using Gauss's theorem, calculate the field due to a thin plane infinite sheet of charge, having a uniform surface charge density $\mathrm{\sigma }$.

---

Consider an infinite thin plane sheet of charge having a uniform surface charge density $\mathrm{\sigma }$ on both sides of sheet. By symmetry, it follows that the electric field is perpendicular to the sheet of charge and is directed in outward direction. 
To find: Electric field due to plane sheet of charge at any point P distant r from it.



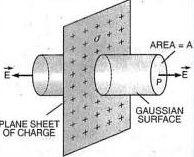
We will draw a cylinder of cross-section area A through the point P as gaussian surface (fig. above).
Electric lines of force are parallel to the curved surface of the cylinder therefore the flux due to electric field of plane sheet of charge passes only through the two circular cross section of cylinder.
If E is the magnitude of electric field at point P, then electric flux crossing through the gaussian surface is

     $$\begin{gathered} \mathrm{\varphi }=\stackrel{\rightharpoonup }{\mathrm{E}}\times \mathrm{area} \mathrm{of} \mathrm{end} \mathrm{faces} (\mathrm{circular} \mathrm{cross} \mathrm{section}) \mathrm{of} \mathrm{the} \mathrm{cylinder} \\ \mathrm{\varphi }=\mathrm{E}\times 2\mathrm{A} \\ \mathrm{According} \mathrm{to} \mathrm{Gauss} \mathrm{theorem}, \mathrm{we} \mathrm{have} \\ \mathrm{\varphi }=\frac{\mathrm{q} }{{\mathrm{\epsilon }}_{\circ }} \\ \mathrm{Here}, \\ \mathrm{the} \mathrm{charge} \mathrm{enclosed} \mathrm{by} \mathrm{the} \mathrm{gaussian} \mathrm{surface} \mathrm{is}-\mathrm{q} = \mathrm{\sigma A} \\ \Rightarrow \mathrm{\varphi }=\frac{\mathrm{\sigma A}}{{\mathrm{\epsilon }}_{\circ }} \\ \Rightarrow \mathrm{E}\times 2\mathrm{A}=\frac{\mathrm{\sigma A}}{{\mathrm{\epsilon }}_{\circ }} \\ \Rightarrow \mathrm{E}=\frac{\mathrm{\sigma }}{2{\mathrm{\epsilon }}_{\circ }} \end{gathered}$$ 
Thus, the magnitude of electric field at a point due to an infinite plane sheet of charge is independent of its distance from the sheet of charge.