Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

 respectively. On the surface of the two spheres, the potential will be



Till the potentials of two conductors become equal the flow of charges continue.
                           

or,          
or,               
Now, the electric field on the two spheres is given as
                   
             
or,      

Therefore, b : a is the ratio of the electric field of the first sphere to that of the second sphere.
The surface charge densities of the two spheres are given as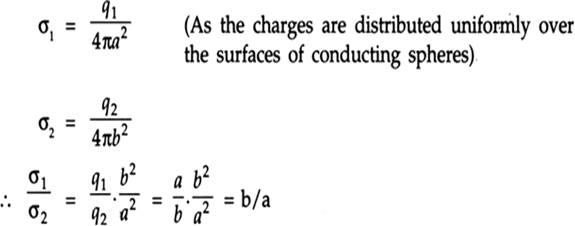


Therefore, the surface charge densities are inversely related with the radii of the sphere. The surface charge density on the sharp and pointed ends of a conductor is higher than on its flatter portion since a flat portion may be taken as a spherical surface of large radius and a pointed portion as that of small radius.