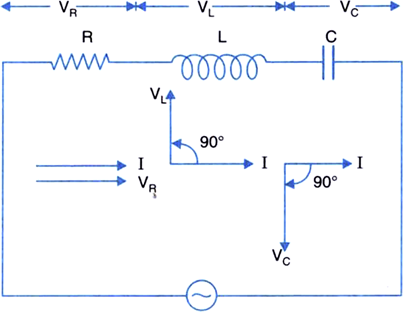
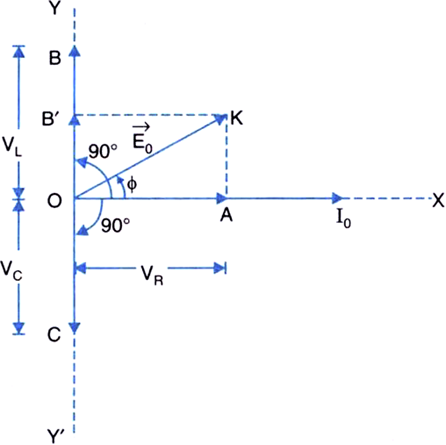
An a.c. source of voltage V = Vm sin ωt is connected, one-by-one, to three circuit elements X, Y and Z. It is observed that the current flowing in them,
(i) is in phase with applied voltage for element X.
(ii) lags the applied voltage, in phase, by /2 for element Y.
(iii) leads the applied voltage, in phase, by /2 for element Z. Identify the three circuit elements.
Find an expression for the (a) current flowing in the circuit, (b) net impedance of the circuit, when the same a.c. source is connected across a series combination of the elements X, Y and Z. (c) If the frequency of the applied voltage is varied, set up the condition of frequency when the current amplitude in the circuit is maximum. Write the expression for this current amplitude.
(For R)
(For L)
) (For C)
is represented along OX.
is in phase with current, it is represented by the vector 
salong OX.
along OY, 90° ahead of 
rotated clockwise through 90° from the direction of 
is along OY' is along OY'.
assuming that 
The resultant of the resultant of 
and 
is the diagonal 
of the rectangle OAKB'. Hence the vector sum of 
is phasor 
represented by 
making an angle 
with current phasor 
