If δ₁ and δ₂ be the angles of dip observed in two planes at right angles to each other and δ is the true angle of dip, then prove that
cot² δ₁ + cot² δ₂ = cot² δ

 respectively, then


Let δ₁ be the (apparent) dip in a plane which makes angle θ with the magnetic meridian. In this plane, the vertical component will be B_V only but the effective horizontal component will be B_H cos θ.
                           
or,                                            
or,                                    ...(i)

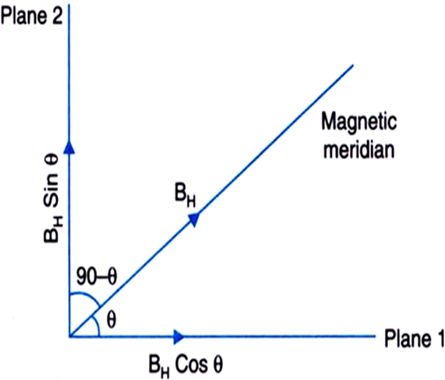
Let δ₂ be the (apparent) dip in the second plane. The angle made by this plane with the magnetic meridian will be (90° – θ).
Effective horizontal component in this plane is B_H cos (90° – θ) i.e., B_H sin θ. The vertical component will be B_v only.
                       
or,                                   ...(ii)
Squaring and adding equation (i) and (ii), we get
                  
or,                       
or,                            Proved