(a) An electric dipole of dipole moment p⃗ consists of point charges +q and –q separated by a distance 2a apart. Deduce the expression for the electric field E⃗ due to the dipole at a distance x from the center of the dipole on its axial line in terms of the dipole moment p⃗. Hence show that in the limit x >> a, E⃗ → 2 p⃗/ (4p ε0 x3).
(b) Given the electric field in the region E⃗ = 2x i, find the net electric flux through the cube and the charge enclosed by it.
Electric field on axial line of an electric dipole is given by,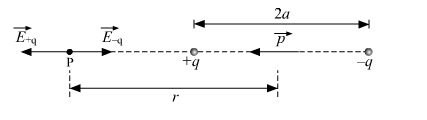 
Suppose, P is a point at distance r from the center of the dipole on the side of charge –q.
Electric field at P due to –q is given by, 
is the unit vector along the dipole axis.
Electric field at P due to +q is given by,
Therefore, total electric field at point P is,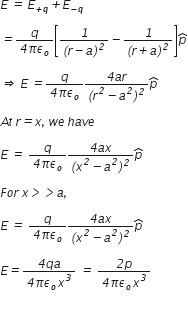
b) Since, the electric field is parallel to the faces parallel to xy and xz planes, the electric flux through them is zero.
Electric flux through the left face,
