We are given a convex mirror.
Here, we have
Object size, h = + 5 cm
Object distance, u = -20 cm
Radius of curvature, R = + 3.0 cm [R is +ve for a convex mirror]
Focal length ,
From mirror formula,
we have,
Image distance,
Magnification,
Therefore,
A virtual and erect image of height 2.2 cm is formed behind the mirror (because v is positive) at a distance of 8.6 cm from the mirror.
A concave lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object placed from the lens? Draw the ray diagram.
Drawing the ray diagram: Using a scale of 1: 5, we get v = - 2 cm, f = - 3 cm. We draw the ray diagram as follows:
(i) Draw the principal axis (a horizontal line).
(ii) Draw a convex lens, keeping principal centre (C) on the principal axis.
(iii) Mark points F and B on the left side of lens at a distance of 3 cm and 2 cm respectively.
(iv) Join any point D (nearly at the top of lens) and F by a dotted line.
(v) Draw a line AD, parallel to principal axis.
![Focal length, f = - 15 cm [f is - ve for a concave lens]Image d](/application/zrc/images/qvar/SCEN10053025-4.png)
(vi) Draw a line A'B', perpendicular to principal axis from B'.
(vii) Draw a line CA', backwards, so that it meets the line from D parallel to principal axis at A.
(viii) Draw a line AB, perpendicular (downwards) from A to meet the principal axis at B.
(ix) The AB is position of object. Measure distance BC. It will be found to be equal to 6 cm.
Thus, object is placed at a distance of 6 cm × 5 = 30 cm from the lens.
Converging lens means a convex lens. As the distances given in the question are large, so we choose a scale of 1: 5, i.e., 1 cm represents 5 cm. Therefore, on this scale 5 cm high object, object distance of 25 cm and focal length of 10 cm can be represented by 1 cm high, 5 cm and 2 cm lines respectively. Now, we draw the ray diagram as follows:
(i) Draw a horizontal line to represent the principal axis of the convex lens.
(ii) Centre line is shown by DE.
(iii) Mark two foci F and F' on two sides of the lens, each at a distance of 2 cm from the lens.
(iv) Draw an arrow AB of height 1 cm on the left side of lens at a distance of 5 cm from the lens.
(v) Draw a line AD parallel to principal axis and then, allow it to pass straight through the focus (F') on the right side of the lens.
(vi) Draw a line from A to C (centre of the lens), which goes straight without deviation.
(vii) Let the two lines starting from A meet at A'.
(viii) Draw AB', perpendicular to the principal axis from A'.
(ix) Now AB', represents the real, but inverted image of the object AB.
(x) Then, measure CB' and A'B'. It is found that CB' = 3.3 cm and A'B' = 0.7 cm.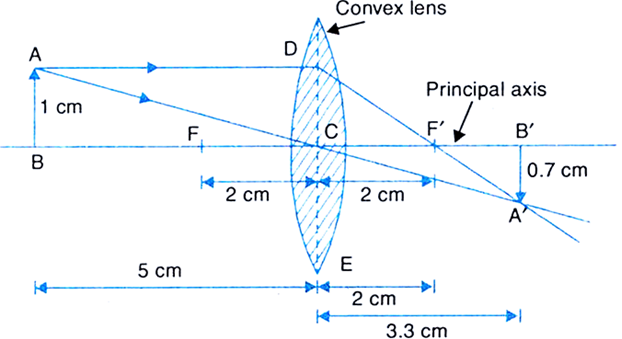
(xi) Thus the final position, nature and size of the image A'B' are:
(a) Position of image A'B' = 3.3 cm × 5 = 16.5 cm from the lens on opposite side.
(b) Nature of image A’B’: Real and inverted.
(c) Height of image A'B': 0.7 × 5 = 3.5 cm, i.e., image is smaller than the object.
We are given a concave mirror.
Here,
Object size, h = + 7.0 cm
Object distance, u = - 27 cm
Focal length, f = - 18 cm
Image distance, v = ?
Image size, h' = ?
Now, using the mirror formula,
i.e.,
The screen should be placed at a distance of 54 cm on the object side of the mirror to obtain a sharp image.
Magnification,
Image size,
The image is real, inverted and enlarged in size.
A concave lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object placed from the lens? Draw the ray diagram.
Focal length, f = - 15 cm [f is - ve for a concave lens]
Image distance, v = - 10 cm [Concave lens forms virtual image on same side as the object, so v is - ve]
As, ![]()
![]()
![]()
Object distance, u = -30 cm. Ans.
Drawing the ray diagram: Using a scale of 1: 5, we get v = - 2 cm, f = - 3 cm. We draw the ray diagram as follows:
(i) Draw the principal axis (a horizontal line).
(ii) Draw a convex lens, keeping principal centre (C) on the principal axis.
(iii) Mark points F and B on the left side of lens at a distance of 3 cm and 2 cm respectively.
(iv) Join any point D (nearly at the top of lens) and F by a dotted line.
(v) Draw a line AD, parallel to principal axis.![Focal length, f = - 15 cm [f is - ve for a concave lens]Image d](/application/zrc/images/qvar/SCEN10053030-3.png)
(vi) Draw a line A'B', perpendicular to principal axis from B'.
(vii) Draw a line CA', backwards, so that it meets the line from D parallel to principal axis at A.
(viii) Draw a line AB, perpendicular (downwards) from A to meet the principal axis at B.
(ix) The AB is position of object. Measure distance BC. It will be found to be equal to 6 cm.
Thus, object is placed at a distance of 6 cm × 5 = 30 cm from the lens.
