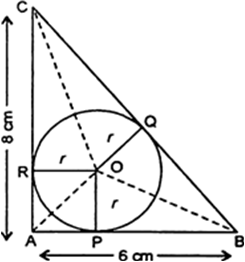
It is given that ABC is a right angle triangle with AB = 6 cm and AC = 8 cm and a circle with centre O has been inscribed.
Using Pythagoras theorem, we get
BC2 = AC2 + AB2
= (8)2 + (6)2
= 64 + 36 = 100
⇒ BC = 10 cm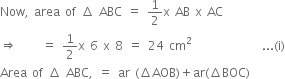
![]() Tangents at any point of a circle is perpendicular to the radius through the point of contact
Tangents at any point of a circle is perpendicular to the radius through the point of contact ![]()
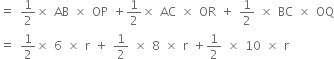
= 3r + 4r + 5r
= 12r ...(ii)
Comparing (i) and (ii), we get
24 = 12r ⇒ r = 2 cm
Method – II:
In quadrilateral APOR,
∵ ∠OPA = ∠ORA = 90°
∠PAR = 90°
⇒ ∠OPA = ∠ORA = ∠PAR = ∠POR = 90° ....(i)
and AP = AR (ii) (length of tangents drawn from an external point are equal)
Using result (i) and (ii), we get
APOR is a square
Therefore,
OR = AR = r [Sides of square] and OR = AP = r [Sides of square]
Now, BP = AB – AP = 6 – r and, CR = AC – AR = 8 – r
Since tangents from an external point are equal
CR = CQ = 8 – r and BP = BQ = 6 – r
Now, In ΔABC,
BC2 = AC2 + AB2
⇒ (CQ + BQ)2 = (8)2 + (6)2
⇒ (8 – r + 6 – r)2 = 64 + 36
⇒ (14 – 2r)2 = 100
⇒ (14 – 2r)2 = (10)2
⇒ 14 – 2r = 10
⇒ –2r = –4
⇒ r = 2
Hence radius of circle (r) = 2 cm.
So, BP = BQ
(Tangents from external point B)
But BP = 27 cm
⇒ BQ = 27 cm
It is given that BC = 38 cm
⇒ BQ + CQ = 38
⇒ 27 + CQ = 38
⇒ CQ = 11 cm
⇒ CQ = CR (Tagents from an external point C)
But CQ = 11 cm
⇒ CR = 11 cm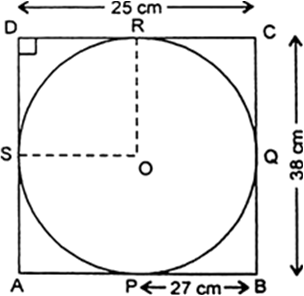
It is given that : CD = 25 cm
⇒ CR + DR = 25
⇒ 11 + DR = 25
⇒ DR = 14 cm
Since, tangent to a circle is perpendicular to the radius through the point of contact.
∴ ∠ORD = ∠OSD = 90°
It is given that
∠D = 90°
Now, in quadrilateral ORDS,
∠ORD = ∠OSD = ∠RDS = ∠ROS = 90°
and OR = OS [radii of circle]
Therefore, ORDS is a square
So, OR = DR = 14 cm
Hence r = 14 cm.
Chord
C.
Secant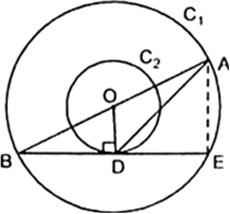
Given : Two concentric circles C1 and C2 of radii 13 cm and 8 cm respectively. AB is a diameter of the bigger circle (C1) and BD is a tangent to the smaller circle (C2).
∴ The tangent at any point of a circle is perpendicular to the radius through the point of contact.![]()
Now, in right triangle BOD, we have
OB2 = OD2 = BD2 [ Using Pythagoras theorem]![]() (13)2 = (8)2 + BD2
(13)2 = (8)2 + BD2 ![]() 169 = 64 + BD2
169 = 64 + BD2 ![]() BD2 = 169 - 64
BD2 = 169 - 64 ![]() BD2 = 105
BD2 = 105![]()
Since, perpendicular drawn from the centre to the chord bisects the chord.
(∵ ∠BEA = 90°, angle in semicircle is right angle] and, ∠OBD = ∠ABE (common)
Therefore, using AAS similar condition ΔBOD ~ ΔBAE![]()
[Proportional sides of two similar triangles]
Now, in right triangle ADE, we have
AD2 = AE2 + DE2 ![]()
= 256 + 105
= 361![]() AD = 19 cm.
AD = 19 cm.
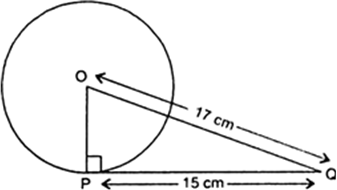
Therefore, ∠OPO =90°
It is given that PQ =15 cm
and OQ = 17 cm
In right ΔOPQ
OQ2 = OP2 + PQ2
[Using Pythagoras theorem]
⇒ (17)2 = OP2 + (15)2
OP2 = (17)2 – (15)2
= 289 – 225 = 64 ⇒ OP = 8 cm
Hence, radius of the circle = 8 cm.
