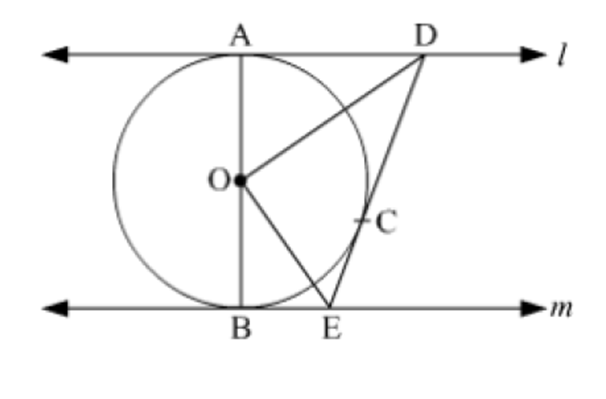
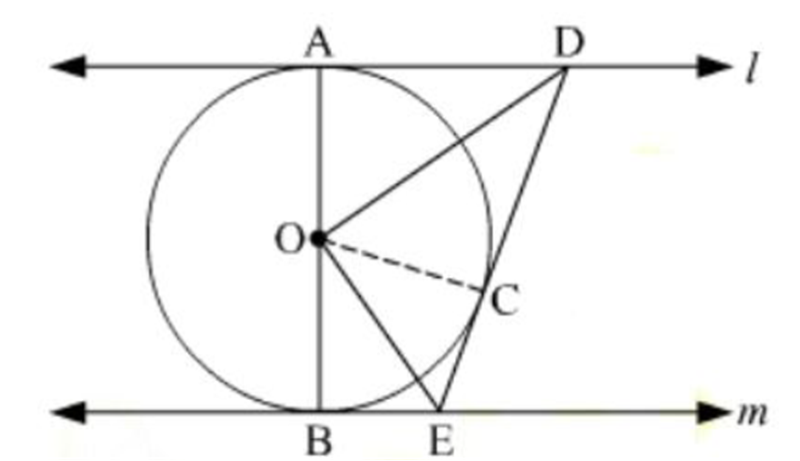
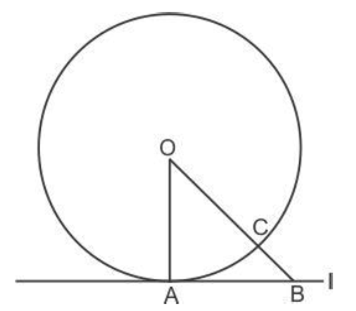
In fig., l and m are two parallel tangents to a circle with centre O,touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that DOE = 900
A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the centre of the circle. Find the area of major and minor segments of the circle.
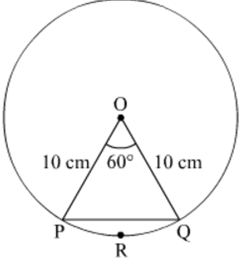
Radius of the circle, r = 10 cm
Area of sector OPRQ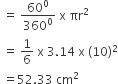
In ΔOPQ,
∠OPQ = ∠OQP (As OP = OQ)
∠OPQ + ∠OQP + ∠POQ = 180°
2∠OPQ = 120°
∠OPQ = 60°
ΔOPQ is an equilateral triangle.
So, area of ΔOPQ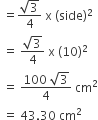
Area of minor segment PRQ
= Area of sector OPRQ − Area of ΔOPQ
= 52.33 − 43.30
= 9.03 cm2
Area of major segment PSQ
= Area of circle − Area of minor segment PRQ
=π(10)2−9.03=314−9.03=304.97 cm2
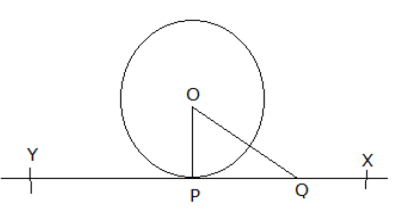
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: A circle C ( 0, r ) and a tangent l at point A.
To prove: OA l
Construction: Take a point B, other than A, on the tangent l. Join OB. Suppose OB meets the circle in C.
Proof: We know that, among all line segment joining the point O to a point on l, the perpendicular is shortest to l.
OA = OC (Radius of the same circle)
Now, OB = OC + BC.
But among all the line segments, joining the point O to a point on AB, the shortest one is the perpendicular from O on AB.
Hence OA is perpendicular to l.
Prove that the tangent at any point of a circle is perpendicular to theradius through the point of contact.
Prove that the lengths of tangents drawn from an external point to a circle are equal.
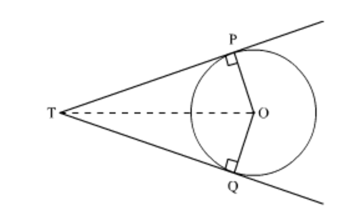
Proof: We know that a tangent to the circle is perpendicular to the radius through the point of contact.
∴ ∠OPT = ∠OQT = 90°
In ΔOPT and ΔOQT,
OT = OT (Common)
OP = OQ (Radius of the circle)
∠OPT = ∠OQT (90°)
∴ ΔOPT ≅ ΔOQT (RHS congruence criterion)
⇒ TP = TQ (CPCT)
Hence, the lengths of the tangents drawn from an external point to a circle are equal.
