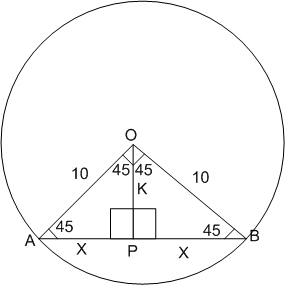
A chord of a circle of radius 10 cm subtends a right angleat its centre. The length of the chord (in cm) is
5
10
10
B.
10
In Fig., a circle touches the side DF of EDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of EDF (in cm) is:

18
13.5
12
9
A.
18
It is known that the tangents from an external point to the circle are equal.
EK = EM, DK = DH and FM = FH .....(1)
Perimeter of EDF = ED + DF + FE
= (EK - DK) + (DH + HF) + EM - FM)
= (EK - DH) + (DH + HF) + (EM - FH) [Using (1)]
= EK + EM
= 2EK = 2(9 CM) = 18 CM
Hence, the perimeter of EDF is 18 cm.
In Fig. , PQ is tangent at point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.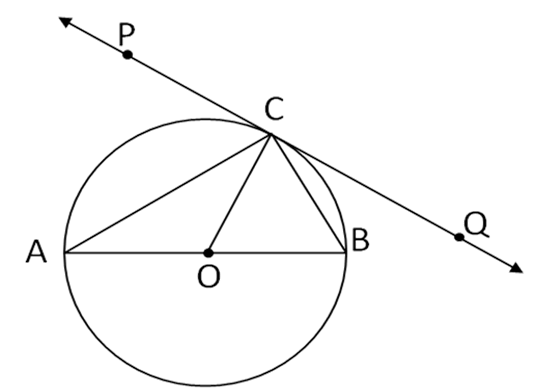
In the given figure,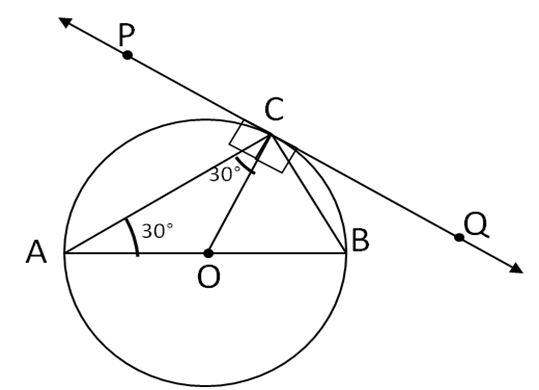
In Δ ACO,
OA=OC (Radii of the same circle)
Therefore,
ΔACO is an isosceles triangle.
∠CAB = 30° (Given)
∠CAO = ∠ACO = 30° (angles opposite to equal sides of an isosceles triangle are equal)
∠PCO = 90° …(radius is drawn at the point of
contact is perpendicular to the tangent)
Now ∠PCA = ∠PCO – ∠CAO
Therefore,
∠PCA = 90° – 30° = 60°
In Fig., the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is

11
10
14
15
B.
10
it is know that the lengths of tangents drwan from a point outside a circle
are equal in length.
Therefore, we have;
AP = AR ........(1) (Tangents drawn from point A)
BP = BQ .........(2) (Tangents drawn from point B)
CQ = CR ..........(3) (Tangents drawn from point C)
Using the above equations,
AR = 4 cm ( AP = 4 cm, given)
BQ = 3 cm ( BP = 3 cm, given)
AC = 11 cm RC = 11 cm - 4 cm = 7 cm
Hence, BC = BQ + CQ = 3 CM + 7 CM = 10 cm.
In Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
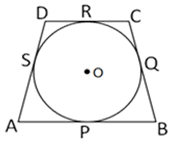
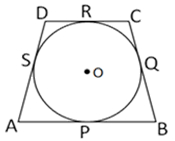
In the Given figure, since tangents are drawn from an exterior point to a circle are equal in length,
AP = AS ….(1)
BP = BQ ….(2)
CR = CQ ….(3)
DR = DS ….(4)
Adding equations (1), (2), (3) and (4), we get
AP + BP + CR + DS = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + CD = BC + DA
Hence proved
