Which of the points is likely position of the centre of mass of the system shown in the figure ?
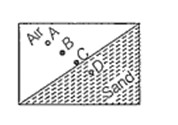
A
D
B
C
B.
D
CM lies towards heavier mass. From figure, it is clear that more mass lies at right side of the given figure. So, centre of mass should be at D.

Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls when in air
is equal to g (acceleration due to gravity)
depends on the speeds of the two balls
depends on the masses of the two balls
depends on the direction of motion of the two balls
A.
is equal to g (acceleration due to gravity)
We know that,
Acceleration of centre of mass
Here, a1 = a2 = g (Because balls are thrown in air i.e, under the gravity)
From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc, about a perpendicular axis, passing through the centre?
13 MR2/32
11MR2/32
9MR2/32
15MR2/32
A.
13 MR2/32
Illustrating the above figure,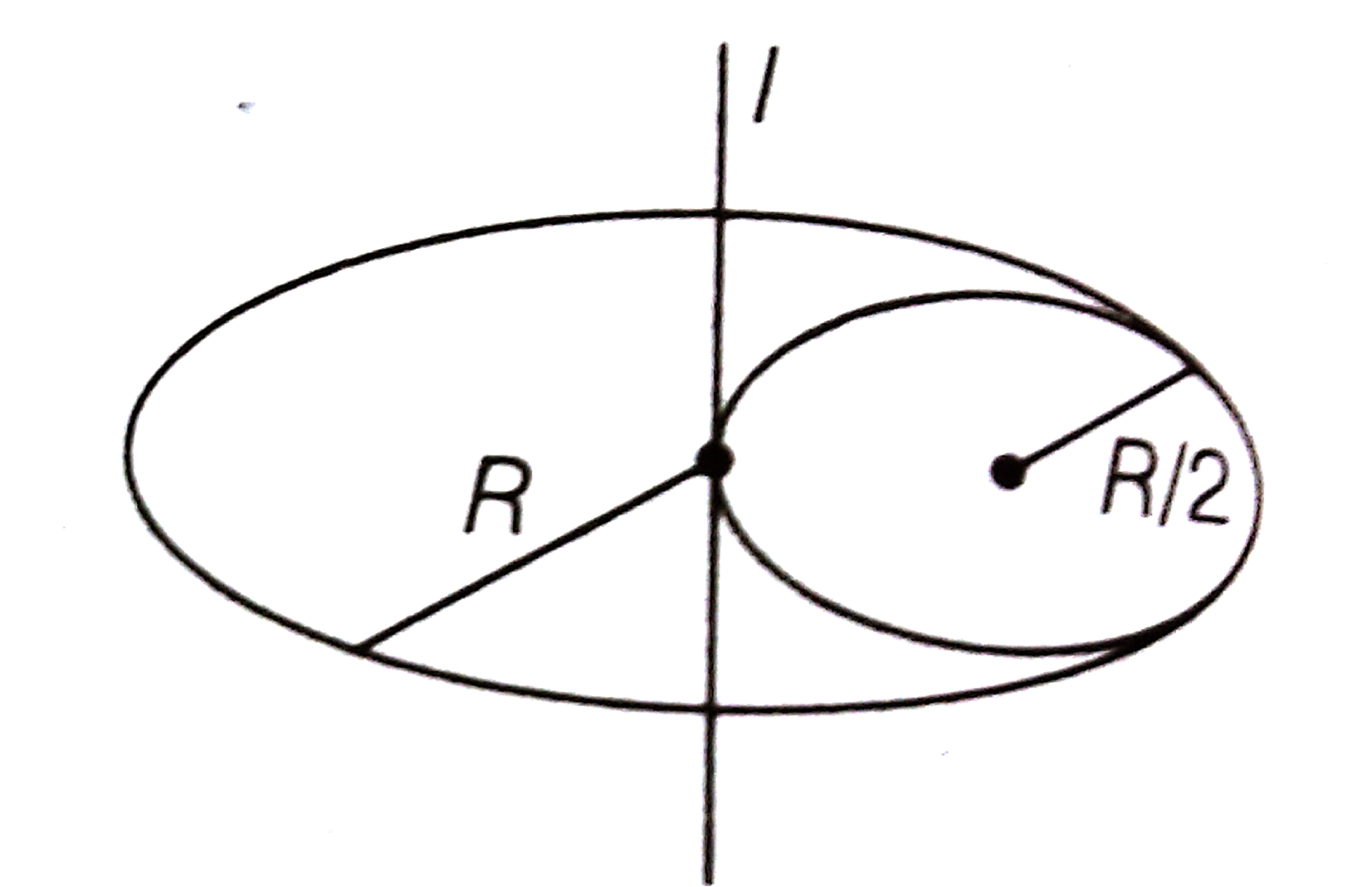
As given in the above fig.,
Moment of Inertia of the disc, I = Iremain + I(R/2)![]()
Now, using the values, we get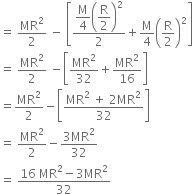
That is,
Iremain = ![]()
The ratio of angular speed of a second-hand to the hour- hand of a watch is
B.
We know that, angular speed of a watch
A disc and a sphere of the same radius but differnt masses roll off two inclined planes of the same altitude and length. which one of the two objects gets to the bottom of the plane first?
Sphere
Both reach at the same time
Depends on their masses
Disc
A.
Sphere
a) Acceleration of an object rolling down an inclined plane is given by,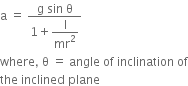
m = mass of the object,
I = moment of Inertia about the axis through the centre of mass.
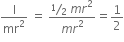
For solid sphere,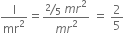
For hollow sphere,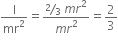
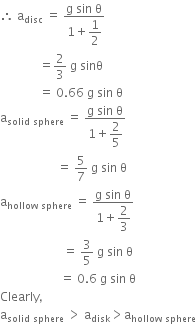
Therefore, the given sphere is a solid sphere.
asolid sphere = ahollow sphere > adisk
