
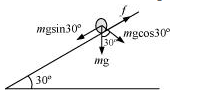
 ...(iii)
...(iii) 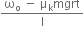 )
) 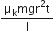 ...(vi)
...(vi)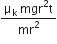
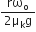
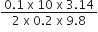
 mr2
mr2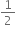 mr2
mr2 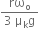
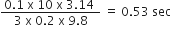 ...(viii)
...(viii) a) False
Frictional force acts opposite to the direction of motion of the centre of mass of a body. In the case of rolling, the direction of motion of the centre of mass is backward. Hence, frictional force acts in the forward direction.
Tips: -
a) Frictional force acts opposite to the direction of motion of the centre of mass of a body. In the case of rolling, the direction of motion of the centre of mass is backward. Hence, frictional force acts in the forward direction.