Given ∆ABC, lines are drawn through A, B and C parallel respectively to the sides
BC, CA and AB forming ∆PQR. Show that BC = ![]()
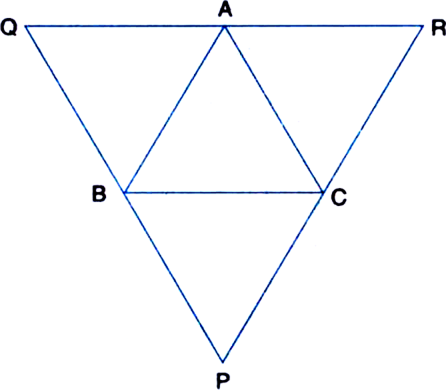
Proof: ∵ AQ || CB and AC || QB
∴ AQBC is a parallelogram
∴ BC = QA ...(1)
| Opposite sides of a ||gm
∵ AR || BC and AB || RC
∴ ARCB is a parallelogram
∴ BC = AR ...(2)
| Opposite sides of a ||gm
From (1) and (2),
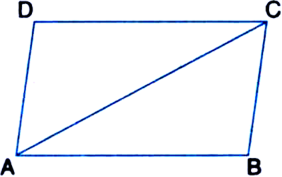
To Prove: ∆ABC ≅ ∆CDA
Proof: BC || DA
| Opposite sides of a parallelogram are parallel
and AC is a transversal
∴ ∠BCA = ∠DAC ...(1)
| Pair of alternate interior angles
Also, AB || DC
Opposite sides of a parallelogram are parallel
and AC is a transversal
∴ ∠BAC = ∠DCA ...(2)
| Pair of alternate interior angles
AC = CA ...(3) | Common
In view of (1), (2) and (3),
∆ABC ≅ ∆CDA
| ASA congruence criterion
Given: ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively.
To Prove: AX || CY.
Proof: ∵ ABCD is a parallelogram.
∴ ∠A = ∠C | Opposite ∠s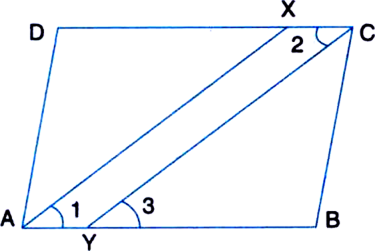
![]()
| ∵ Halves of equals are equal
⇒ ∠1 = ∠2 ....(1)
| ∵ AX is the bisector of ∠A and CY is the bisector of ∠C
Now, AB || DC and CY intersects them
∴ ∠2 = ∠3 ...(2)
| Alternate interior ∠s
From (1) and (2), we get
∠1 = ∠3
But these form a pair of equal corresponding angles
∴ AX || CY.
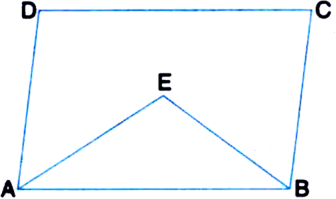
To Prove: ∠AEB = 90°
Proof: ∵ AD || BC
| Opposite sides of ||gm and transversal AB intersects them
∴ ∠DAB + ∠CBA = 180°
| ∵ Sum of consecutive interior angles on the same side of a transversal is 180°
⇒ 2∠EAB + 2∠EBA = 180°
| ∵ AE and BE are the bisectors of ∠DAB and ∠CBA respectively.
⇒ ∠EAB + ∠EBA = 90° ...(1)
In ∆EAB,
∠EAB + ∠EBA + ∠AEB = 180°
| ∵ The sum of the three angles of a triangle is 180°
⇒ 90° + ∠AEB = 180° | From (1)
⇒ ∠AEB = 90°.
B.
Diagonals of a rhombus are perpendicular to each other