
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
For a brick
l = 22.5 cm b = 10 cm h = 7.5 cm
∴ Total surface area of a brick = 2 (lb + bh + hl)
= 2(22.5 x 10 + 10 x 7.5 + 7.5 x 22.5)
= 2(225 + 75 + 168.75)
= 2(468.75) = 937.5 cm2 = .09375 m2
∴ Number of bricks that can be painted out![]()
l = 5 m
b = 4 m
h = 3 m
Area of the walls of the room = 2(l + b) h
= 2(5 + 4) 3 = 54 m2
Area of the ceiling = lb
= (5) (4) = 20 m2
∴ Total area of the walls of the room and the ceiling = 54 m2 + 20 m2 = 74 m2
∴ Cost of white washing the walls of the room and the ceiling = 74 x 7.50 = र 555.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ` 10 per m2 is ` 15000, find the height of the hall. [Hint : Area of the four walls = Lateral surface area.]
Let the length, breadth and height of the rectangular hall be l m, b m and h m respectively.
Perimeter = 250 m
⇒ 2(l + b) = 250
⇒ l + b = 125 ...(1)
Area of the four walls
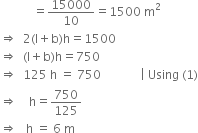
Hence, the height of the hall is 6 m.
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costsर 20.
(i) l = 1.5 m
b= 1.25 m
h = 65 cm = 0.65 m.
∴ The area of the sheet required for making the box = lb + 2(bh + hl)
= (1.5)(1.25) + 2 {(1.25)(0.65) + (0.65)(1.5)} = 1.875 + 2{0.8125 + 0.975}
= 1.875 + 2(1.7875) = 1.875 + 3.575 = 5.45 m2.
(ii) The cost of sheet for it = र 5.45 x 20 = र 109.
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
Each edge of the cubical box (a) = 10 cm
∴ Lateral surface area of the cubical box = 4a2 = 4(10)2 = 400 cm2.
For cuboidal box
l = 12.5 cm b = 10 cm h = 8 cm
Lateral surface area of the cuboidal box = 2(l + b) h
= 2(12.5+ 10)(8) = 360 cm2.
∴ Cubical box has the greater lateral surface area than the cuboidal box by (400 – 360) cm2, i.e., 40 cm2.
