 Multiple Choice Questions
Multiple Choice QuestionsConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume ![]() and pressure.
and pressure.![]() If the shell now undergoes an adiabatic expansion the relation between T and R is
If the shell now undergoes an adiabatic expansion the relation between T and R is
T ∝ e-R
T ∝ e-3R
T ∝ (1/R)
T ∝(1/R3)
A solid body of constant heat capacity 1 J/°C is being heated by keeping it in contact with reservoirs in two ways:
(i) Sequentially keeping in contact with 2 reservoirs such that each reservoir supplies the same amount of heat.
(ii) Sequentially keeping in contact with 8 reservoirs such that each reservoir supplies the same amount of heat. In both the cases body is brought from an initial temperature 100°C to final temperature 200°C. Entropy change of the body in the two cases respectively is:
ln2,4ln2
ln2,ln2
ln2,2ln2
2ln2,8ln2
Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion the average time of collision between molecules increases as Vq , where V is the volume of the gas. The value of q is: 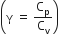
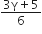
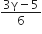
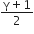
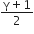
One mole of diatomic ideal gas undergoes a cyclic process ABC as shown in the figure. The process BC is adiabatic. The temperatures at A, B and C are 400 K, 800 K and 600 K respectively. Choose the correct statement:
The change in internal energy in the process AB is -350 R.
The change in internal energy in the process BC is -500 R.
The change in internal energy in the whole cyclic process is 250 R.
The change in internal energy in the whole cyclic process is 250 R.
The above p-v diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat extracted from the source in a single cycle is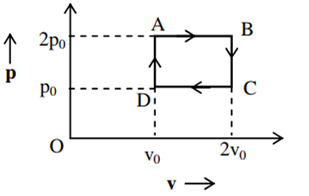
povo
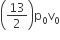
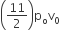
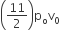
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
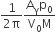
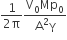
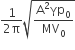
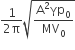
A Carnot engine, whose efficiency is 40%, takes in heat from a source maintained at a temperature of 500 K It is desired to have an engine of efficiency 60%. Then, the intake temperature for the same exhaust (sink) temperature must be
the efficiency of Carnot engine cannot be made larger than 50%
1200 K
750 K
750 K
Helium gas goes through a cycle ABCDA (consisting of two isochoric and two isobaric lines) as shown in the figure. Efficiency of this cycle is nearly:(Assume the gas to be close to ideal gas)
15.4%
9.1%
10.5%
10.5%
Three perfect gases at absolute temperature T1, T2 and T3 are mixed. The masses of molecules are m1,m2 and m3 and the number of molecules is n1,n2 and n3 respectively.Assuming no loss of energy, the final temperature of the mixture is
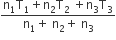
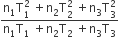
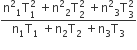
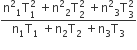
A Carnot engine operating between temperatures T1 and T2 has efficiency 1/6. When T2 is lowered by 62 K, its efficiency increases to 1/3. Then T1 and T2 are, respectively
372 K and 330 K
330 K and 268 K
310 K and 248 K
310 K and 248 K
