Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

421.

Find the equation of tangent to the curve x = sin 3t, y = cos 2t, at t = $\frac{π}{4}$

422.

Show that the rectangle of maximum area that can be inscribed in a circle is a square.

423.
Show that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is $\frac{1}{3}$ h.

Let a cylinder be inscribed in a cone of radius R and height h.

Let a radius of the cylinder be r and its height be h₁.

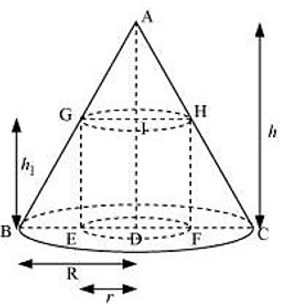
It can be easily seen that $∆$ AGI and $∆$ ABD are similar.

$∴ \frac{AI}{AD} = \frac{GI}{BD} \Rightarrow \frac{h - h_{1}}{h} = \frac{r}{R} \Rightarrow r = \frac{R}{h} h - h_{1} Volume (V) of the cylinder = {πr}^{2} h_{1} \Rightarrow V = π \frac{R^{2}}{h^{2}} (h - h_{1})^{2} h_{1} \Rightarrow V = π \frac{R^{2}}{h^{2}} [h^{2} + {h_{1}}^{2} - 2 {hh}_{1}] x h_{1} \Rightarrow \frac{dv}{{dh}_{1}} = π \frac{R^{2}}{h^{2}} [h^{2} + {h_{1}}^{2} - 2 {hh}_{1} + h_{1} (2 h_{1} - 2 h)] \Rightarrow \frac{dv}{{dh}_{1}} = π \frac{R^{2}}{h^{2}} (h^{2} + 3 {h_{1}}^{2} - 4 {hh}_{1})$

$Now, \frac{dV}{{dh}_{1}} = 0 \Rightarrow \frac{{πR}^{2}}{h^{2}} (h^{2} + 3 {h_{1}}^{2} - 4 {hh}_{1}) = 0 \Rightarrow 3 {h_{1}}^{2} - 4 {hh}_{1} + h^{2} = 0 \Rightarrow 3 {h_{1}}^{2} - 3 {hh}_{1} - {hh}_{1} + h^{2} = 0 \Rightarrow 3 h_{1} (h_{1} - h) - h (h_{1} - h) = 0 \Rightarrow (h_{1} - h) (3 h_{1} - h) = 0 \Rightarrow h_{1} = h, h_{1} = \frac{h}{3}$

It can be noted that if h₁ = h, then the cylinder cannot be inscribed in the cone.

$∴ h_{1} = \frac{h}{3} Now, \frac{d^{2} V}{{dh}_{1}^{2}} = \frac{{πR}^{2}}{h^{2}} 0 + 6 h_{1} - 4 h = \frac{{πR}^{2}}{h^{2}} 6 h_{1} - 4 h ∴ {\frac{d^{2} V}{{dh}_{1}^{2}}}_{(h_{1} = \frac{h}{3})} = \frac{{πR}^{2}}{h^{2}} [\frac{6 h}{3} - 4 h] = \frac{- 2 {πR}^{2}}{h} < 0$

Therefore, by the second derivative test, h₁ = $\frac{h}{3}$ is the point of local maxima of V.

So, the volume of the cylinder is the maximum when h₁ = $\frac{h}{3}$ .

Hence, the height of the cylinder of the maximum volume that can be inscribed in a cone of height h is $\frac{1}{3} h$ .

424.

Find the equation of the tangent to the curve $y = \sqrt{3 x - 2}$ which is parallel to the line 4x – 2y + 5 = 0

425.

Find the intervals in which the function f given by $f (x) = x^{3} + \frac{1}{x^{3}}, x \neq 0$ is

(i) increasing

(ii) decreasing.

426.

Find the volume of the largest cylinder that can be inscribed in a sphere of radius r.

427.

A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m³. If building of tank costs Rs. 70 per square metre for the base and Rs. 45 per square metre for sides, what is the cost of least expensive tank?

428.

Find the equations of the normals to the curve y = x³ + 2x + 6 which are parallel to the line x + 14y + 4 = 0.

429.

Find the values of x for which f(x) = [x(x - 2)]2 is an increasing function. Also, find the points on the curve where the tangent is parallel to x-axis.

430.

Show that the right circular cylinder, open at the top, and of given surface area and maximum volume is such that its height is equal to the radius of the base.

Previous Year Papers

Test Series

Test Yourself

Long Answer Type

423. Show that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is 13h.

423.
Show that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is $\frac{1}{3}$ h.