 Multiple Choice Questions
Multiple Choice QuestionsA wire of length 2 units is cut into two parts which are bent respectively to form a square of side=x units and a circle of radius=r units. If the sum of the areas of the square and the circle so formed is minimum, then:
2x=(π+4)r
(4−π)x=πr
x=2r
x=2r
Let f (x) be a polynomial of degree four having extreme values at x =1 an x =2. If 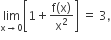 then f(2) is equal to
then f(2) is equal to
-8
-4
0
0
C.
0
Any function have extreme values (maximum and minimum) at its critical points, where f'(x)= 0
Since, the function have extreme values at x =1 and x=2
therefore, f'(x) = 0 at x =1 and x= 2
⇒ f'(1) = 0 and f'(2) = 0
Also, it is given that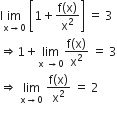
⇒ f(x) will be of the form
ax4 + bx3 + 2x4
f(x) is four degree polynomial]
Let f(x) = ax4 +bx3 +2x2
⇒ f'(x) = 4ax3 + 3bx2+ 4x
⇒ f'(1) = 4a +3b+4 = 0
and f'(2) 32a + 12b +8 = 0
⇒ 8a + 3b + 2 = 0
On solving Eqs. (i) and (ii), we get
a = 1/2, b = -2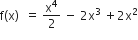
f(2) = 8 - 16 +8 = 0
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is
9/7
7/9
2/9
2/9
Let a, b ∈ R be such that the function f given by f(x) = ln |x| + bx
2+ ax, x ≠ 0 has extreme values at x = –1 and x = 2.
Statement 1: f has local maximum at x = –1 and at x = 2.
Statement 2: 
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Equation of the ellipse whose axes are the axes of coordinates and which passes through the point (-3, 1) and has eccentricity  is
is
3x2 + 5y2 -32 = 0
5x2 + 3y2 - 48 = 0
3x2 + 5y2 - 15 = 0
3x2 + 5y2 - 15 = 0
The two circles x2 + y2 = ax and x2 + y2 = c2(c > 0) touch each other if
2|a| = c
|a| = c
a = 2c
a = 2c
If two tangents drawn from a point P to the parabola y2= 4x are at right angles, then the locus of P is
X = 1
2x +1 = 0
x = -1
x = -1
The radius of a circle, having minimum area, which touches the curve y = 4 – x2 and the lines, y = |x| is
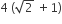
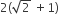
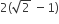
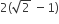
Let y be an implicit function of x defined by x2x – 2xxcoty – 1 = 0. Then y′ (1) equals
-1
1
log 2
log 2
