Given P(x) = x⁴+ ax³ + cx + d such that x = 0 is the only real root of P′ (x) = 0. If P(–1) < P(1),then in the interval [–1, 1].

• P(–1) is the minimum and P(1) is the maximum of P

• P(–1) is not minimum but P(1) is the maximum of P

• P(–1) is the minimum but P(1) is not the maximum of P

• P(–1) is the minimum but P(1) is not the maximum of P

Suppose the cube x³– px + q has three distinct real roots where p > 0 and q > 0. Then which one of the following holds?

• The cubic has minima at  and maxima at –

• The cubic has minima at – and maxima at

• The cubic has minima at both  and- 

• The cubic has minima at both  and- 

The differential equation of the family of circles with fixed radius 5 units and centre on the line y = 2 is 

• (x – 2)y′² = 25 – (y – 2)² 

• (y – 2)y′² = 25 – (y – 2)²

• (y – 2)²y′²= 25 – (y – 2)² 

• (y – 2)²y′²= 25 – (y – 2)² 

454.

The function f(x) = tan^-1 (sinx + cosx) is an increasing function in

• (π/4, π /2)

• (–π/2, π /4)

• (0, π /2)

• (0, π /2)

If 

• x /x+1

• x-1/x

• 1/x

• 1/x

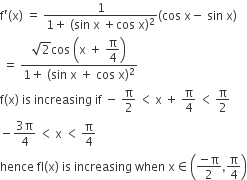
The normal to the curve x = a(1 + cosθ), y = asinθ at ‘θ’ always passes through the fixed point

• (a, 0)

• (0, a)No

• (0,0)

• (0,0)

let y = y(x) be the solution of the differential equation $\sin x \frac{dy}{dx} + y \cos x = 4x, x\in (0, \pi )$. If $y = \left(\frac{\pi }{2}\right) = 0, then y\left(\frac{\pi }{6}\right) is equal to:$

• $-\frac{4}{9}{\pi }^2$

• $\frac{4}{9\sqrt{3}}{\pi }^2$

• $\frac{-8}{9\sqrt{3}}{\pi }^2$

• $-\frac{8}{9}{\pi }^2$

If the line ax + by + c = 0, ab $\ne$ 0, is a tangent to the curve xy = 1- 2x, then

• a> 0, b < 0

• a>0, b> 0

• a< 0, b > 0

• a< 0, b < 0

Time period T of a simple pendulum of length l is given by T = $2\mathrm{\pi }\sqrt{\frac{1}{\mathrm{g}}}$. If the length is increased by 2%, then an approximate change in the time period is

• 2 %

• 1 %

• $\frac{1}{2}$ %

• None of these

The number of values of k, for which the equation x² - 3x + k=0 has two distinct roots lying in the interval (0, 1), are

• three

• two

• infinitely many

• no value of k satisfies the requirement