 Multiple Choice Questions
Multiple Choice QuestionsA variable circle passes through the fixed point A (p, q) and touches x-axis. The locus of the other end of the diameter through A is
(x-p)2 = 4qy
(x-q)2 = 4py
(y-p)2 = 4qx
(y-p)2 = 4qx
If the lines 2x + 3y + 1 = 0 and 3x – y – 4 = 0 lie along diameters of a circle of circumference 10π, then the equation of the circle is
x2 + y2- 2x +2y -23 = 0
x2 - y2- 2x -2y -23 = 0
x2 - y2- 2x -2y +23 = 0
x2 - y2- 2x -2y +23 = 0
If a ≠ 0 and the line 2bx + 3cy + 4d = 0 passes through the points of intersection of the parabolas y2+ 4ax = and x2+ 4ay = , then
d2 + (2b+3c)2 = 0
d2 +(3d+2c2) = 0
d2 + (2b-3c)2 = 0
d2 + (2b-3c)2 = 0
The eccentricity of an ellipse, with its centre at the origin, is 1 /2 . If one of the directrices is x = 4, then the equation of the ellipse is
3x2 +4y2 = 1
3x2+ 4y2 = 12
4x2 +3y2 = 12
4x2 +3y2 = 12
PQR is a triangular park with PQ = PR = 200 m. A T.V. tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P, Q and R are respectively 45o, 30o and 30o, then the height of the tower (in m) is
50√2
100
50
100√3
Tangents are drawn to the hyperbola 4x2 – y2 = 36 at the points P and Q. If these tangents intersect at the point T(0, 3) then the area (in sq. units) of △PTQ is
36√5
45√5
54√3
60√3
Tangent and normal are drawn at P(16, 16) on the parabola y2 = 16x, which intersect the axis of the
parabola at A and B, respectively. If C is the centre of the circle through the points P, A and B and,∠CPB = θ then a value of tan θ is
4/3
1/2
2
3
A straight line through a fixed point (2, 3) intersects the coordinate axes at distinct points P and Q. If O is the origin and the rectangle OPRQ is completed, then the locus of R is
3x + 2y = 6xy
3x + 2y = 6
2x + 3y = xy
3x + 2y = xy
Let P be the foot of the perpendicular from focus S of hyperbola on the line bx- ay = 0 and let C be the centre of the hyperbola. Then, the area of the rectangle whose sides are equal to that of SP and CP is
2ab
ab
B.
ab
Given, equation of hyperbola is,
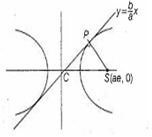
From figure,
SP =
=
And, CS = ae
Again, SPC is right angled triangle at P.
=
=
=
= a
Area of rectangle = GP x SP
= ab
B is an extremity of the minor axis of an ellipse whose foci are S and S'. If SBS' is a right angle, then the eccentricity of the ellipse is
