For the given differential equation, find the particular solut

Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Advertisement

Differential Equations

Short Answer Type

221.

Solve:
$straight y apostrophe space equals space straight y over straight x plus sin straight y over straight x$

78 Views

222.

Solve:
$dy over dx space equals straight y over straight x plus tan straight y over straight x open parentheses 0 less than straight y over straight x less than straight pi over 2 close parentheses$

74 Views

Long Answer Type

223.

For the given differential equations, find the particular solution satisfying the given condition:
$left parenthesis straight x plus straight y right parenthesis space dy space plus space left parenthesis straight x minus straight y right parenthesis dx space equals space 0 space semicolon space space straight y space equals space 1 space space space when space straight x space equals space 1$

75 Views

224.

For the given differential equation, find the particular solution satisfying the given condition:
$straight x squared dy plus left parenthesis xy plus straight y squared right parenthesis dx space equals space 0 semicolon space space space straight y space equals space 1 space when space straight x space equals space 1$

80 Views

Advertisement

225.

For the given differential equation, find the particular solution satisfying the given condition:
$open square brackets straight x space sin squared open parentheses straight y over straight x close parentheses minus straight y close square brackets space dx plus space straight x space dy space equals space 0 colon space space space straight y space equals straight pi over 4 space space when space straight x space equals space 1$

73 Views

226.

For the given differential equation, find the particular solution satisfying the given condition:
$dy over dx minus straight y over straight x plus cosec space open parentheses straight y over straight x close parentheses space equals space 0 space semicolon space space space straight y space equals space 0 space space space when space straight x space equals space 1$

75 Views

227.

For the given differential equation, find the particular solution satisfying the given condition:
$2 xy plus straight y squared minus 2 straight x squared dy over dx equals 0 semicolon space space space straight y space equals 2 space space when space straight x space equals space 1.$

75 Views

228.

For the given differential equation, find the particular solution satisfying the given condition:
$2 straight x squared straight y apostrophe space minus space 2 xy plus straight y squared space equals space 0 comma space space space space straight y left parenthesis straight e right parenthesis space equals space straight e$

74 Views

Advertisement

Advertisement

229.
For the given differential equation, find the particular solution satisfying the given condition:
$2 xy plus straight y squared minus 2 straight x squared straight y apostrophe space equals space 0 space space space space space space space space space space space space space straight y left parenthesis 1 right parenthesis space equals space 2$

The given differential equation is

2 xy plus straight y squared minus 2 straight x squared straight y apostrophe space equals space 0 space space space space space space space or space space space space space 2 straight x squared straight y apostrophe space equals space 2 xy plus straight y squared

therefore space space space space space space space space space dy over dx space equals space fraction numerator 2 xy plus straight y squared over denominator 2 straight x squared end fraction

Put y - v x so that

dy over dx equals straight v plus straight x dv over dx

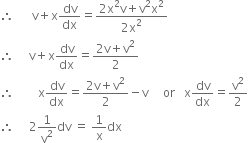
therefore space space space space space space straight v plus straight x dv over dx equals fraction numerator 2 straight x squared straight v plus straight v squared straight x squared over denominator 2 straight x squared end fraction therefore space space space space space straight v plus straight x dv over dx equals fraction numerator 2 straight v plus straight v squared over denominator 2 end fraction therefore space space space space space space space space straight x dv over dx equals fraction numerator 2 straight v plus straight v squared over denominator 2 end fraction minus straight v space space space space space or space space space straight x dv over dx equals straight v squared over 2 therefore space space space space space 2 1 over straight v squared dv space equals space 1 over straight x dx

Integration,

2 space integral straight v to the power of negative 2 end exponent space dv space equals space integral 1 over straight x dx

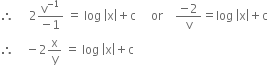
therefore space space space space space 2 fraction numerator straight v to the power of negative 1 end exponent over denominator negative 1 end fraction space equals space log space open vertical bar straight x close vertical bar plus straight c space space space space space or space space space space fraction numerator negative 2 over denominator straight v end fraction equals log space open vertical bar straight x close vertical bar plus straight c therefore space space space space minus 2 straight x over straight y space equals space log space open vertical bar straight x close vertical bar plus straight c

Now,

straight y left parenthesis 1 right parenthesis space equals space 2 space space space space space space space space space space space space space space rightwards double arrow space space space space straight y space equals space 2 space space space when space straight x space equals space 1

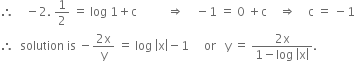
therefore space space space space minus 2. space 1 half space equals space log space 1 plus straight c space space space space space space space space space space rightwards double arrow space space space space minus 1 space equals space 0 space plus straight c space space space space rightwards double arrow space space space space straight c space equals space minus 1 therefore space space solution space is space minus fraction numerator 2 straight x over denominator straight y end fraction space equals space log space open vertical bar straight x close vertical bar minus 1 space space space space space or space space space straight y space equals space fraction numerator 2 straight x over denominator 1 minus log space open vertical bar straight x close vertical bar end fraction.

73 Views

Advertisement

Short Answer Type

230.

Find a particular solution of the differential equation
(x – y) (dx + dy) = dx – dy. given that y = – 1, when x = 0.

75 Views

Advertisement